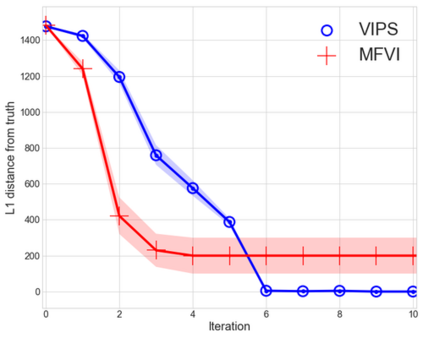
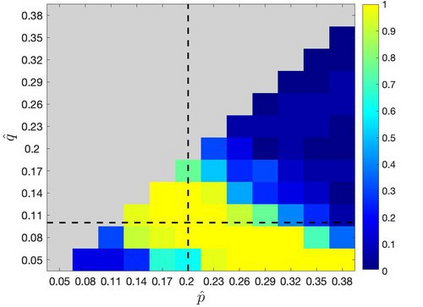
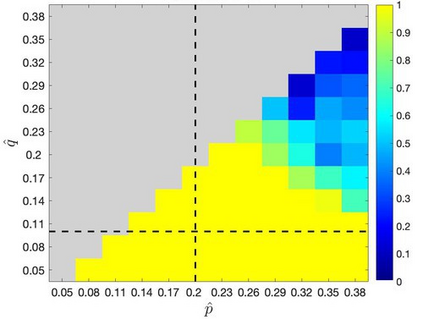
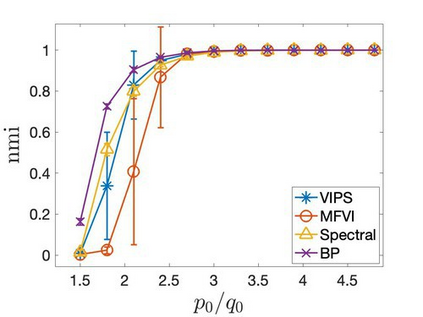
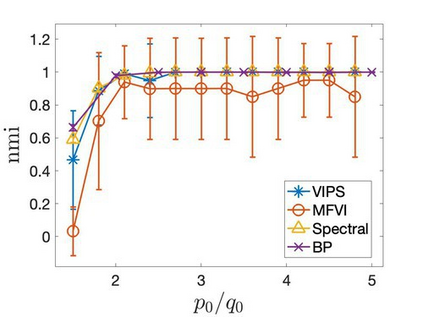
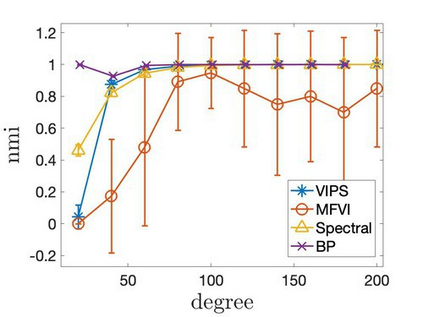
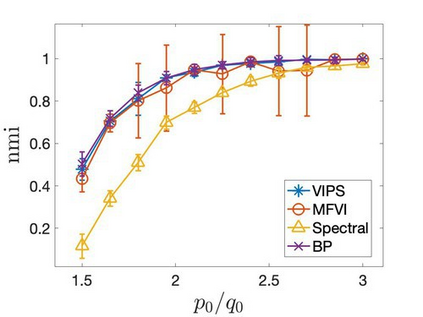
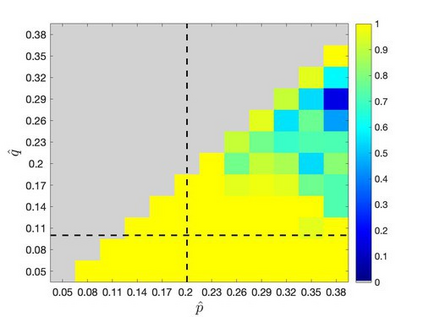
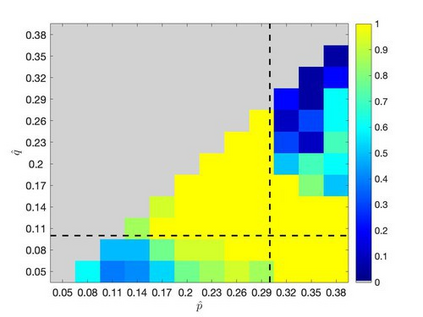
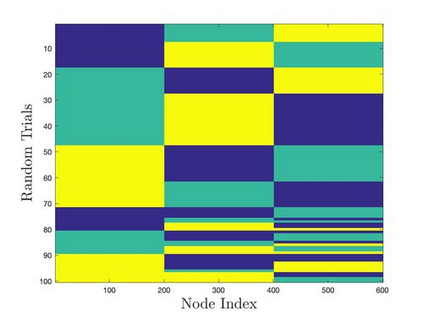
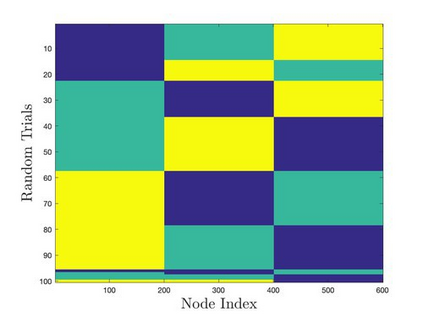
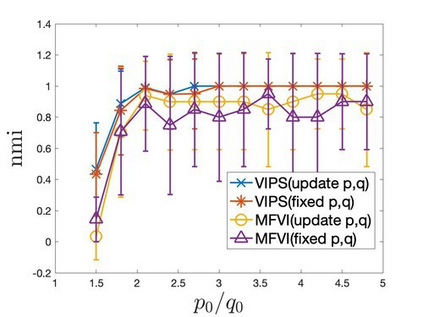
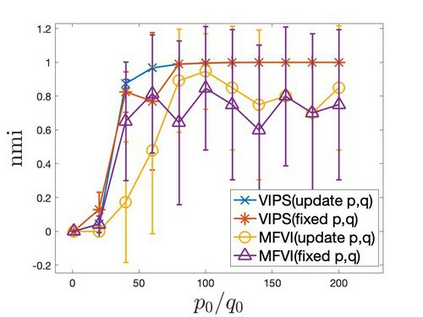
Mean-field variational inference (MFVI) has been widely applied in large scale Bayesian inference. However MFVI, which assumes a product distribution on the latent variables, often leads to objective functions with many local optima, making optimization algorithms sensitive to initialization. In this paper, we study the advantage of structured variational inference for the two class Stochastic Blockmodel. The variational distribution is constructed to have pairwise dependency structure on the nodes of the network. We prove that, in a broad density regime and for general random initializations, unlike MFVI, the class labels estimated from our method converge to the ground truth with high probability, when the model parameters are known, estimated within a reasonable range or jointly optimized with the variational parameters. In addition, empirically we demonstrate structured VI is more robust compared with MFVI when the graph is sparse and the signal to noise ratio is low. The paper takes a first step towards understanding the importance of dependency structure in variational inference for community detection.
翻译:在大型贝叶斯推断中,广泛应用了平均场变率(MFVI),然而,假定潜在变量产品分布的MFVI(MFVI)往往导致与许多局部选取有关的客观功能,使优化算法对初始化十分敏感。在本文中,我们研究了两大类软体块模型结构化变率(MFVI)的优势。变差分布的构建是为了对网络节点有双向依赖结构。我们证明,与MFVI不同的是,在广密度制度和一般随机初始化中,当模型参数已知、在合理范围内估计或与变异参数共同优化时,我们估算的类别标签极有可能与地面真理相融合。此外,在图表稀少、噪音信号低时,我们从经验上表明结构六比MFVI更为坚固。我们迈出了第一步,以了解在社区检测变异推中依赖结构的重要性。