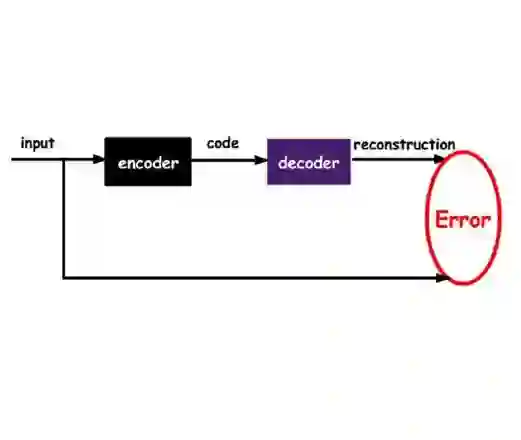
Autoencoders are a popular model in many branches of machine learning and lossy data compression. However, their fundamental limits, the performance of gradient methods and the features learnt during optimization remain poorly understood, even in the two-layer setting. In fact, earlier work has considered either linear autoencoders or specific training regimes (leading to vanishing or diverging compression rates). Our paper addresses this gap by focusing on non-linear two-layer autoencoders trained in the challenging proportional regime in which the input dimension scales linearly with the size of the representation. Our results characterize the minimizers of the population risk, and show that such minimizers are achieved by gradient methods; their structure is also unveiled, thus leading to a concise description of the features obtained via training. For the special case of a sign activation function, our analysis establishes the fundamental limits for the lossy compression of Gaussian sources via (shallow) autoencoders. Finally, while the results are proved for Gaussian data, numerical simulations on standard datasets display the universality of the theoretical predictions.
翻译:自动编码器是机器学习和数据压缩的许多分支中流行的模型。然而,它们的基本局限性、梯度方法的性能和优化过程中所学到的特征仍然不甚为人知,即使在两层环境中也是如此。事实上,早期的工作既考虑了线性自动编码器,也考虑了具体的培训制度(导致压缩率消失或差异 ) 。我们的论文通过侧重于非线性双层自动编码器来解决这一差距,在具有挑战性的比例制中,经过培训的输入维度与代表体的大小线性成比例制。我们的结果是人口风险最小化的特征,并表明这种最小化是用梯度方法实现的;它们的结构也被揭开,从而导致对通过培训获得的特征的简明描述。对于标志激活功能的特殊案例,我们的分析为通过(shallow)自动编码器对高斯源进行损失压缩规定了基本限度。最后,虽然对高斯的数据进行了验证,但标准数据集的数值模拟显示了理论预测的普遍性。