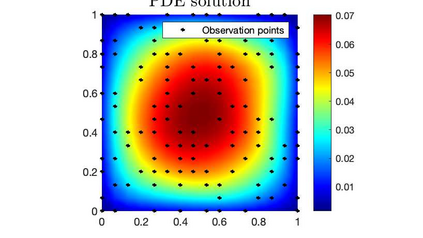
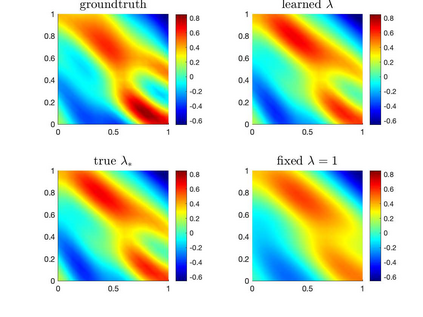
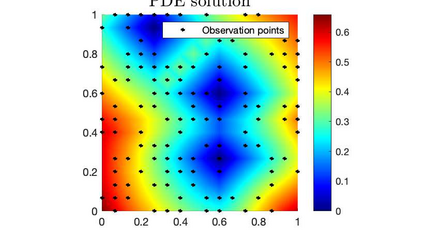
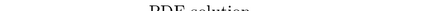One fundamental problem when solving inverse problems is how to find regularization parameters. This article considers solving this problem using data-driven bilevel optimization, i.e. we consider the adaptive learning of the regularization parameter from data by means of optimization. This approach can be interpreted as solving an empirical risk minimization problem, and we analyze its performance in the large data sample size limit for general nonlinear problems. We demonstrate how to implement our framework on linear inverse problems, where we can further show the inverse accuracy does not depend on the ambient space dimension. To reduce the associated computational cost, online numerical schemes are derived using the stochastic gradient descent method. We prove convergence of these numerical schemes under suitable assumptions on the forward problem. Numerical experiments are presented illustrating the theoretical results and demonstrating the applicability and efficiency of the proposed approaches for various linear and nonlinear inverse problems, including Darcy flow, the eikonal equation, and an image denoising example.
翻译:在解决反向问题时,一个根本的问题是如何找到正规化参数。 本条考虑使用数据驱动双层优化来解决这个问题, 即我们考虑通过优化从数据中从数据中适应性地学习正规化参数。 这种方法可以被解释为解决实证风险最小化问题, 并分析它在非线性一般问题大数据样本大小限制中的性能。 我们演示如何在线性反向问题上实施我们的框架, 我们可以进一步显示反向准确性并不取决于环境空间层面。 为了降低相关的计算成本, 使用随机梯度下行法来计算在线数字计划。 我们证明这些数字计划在对前期问题的适当假设下是趋同的。 数字实验展示了理论结果, 并展示了各种线性和非线性问题的拟议方法的适用性和有效性, 包括达西流、 ekonal 方程式和图像分辨示例。