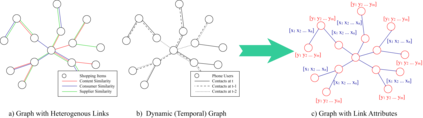
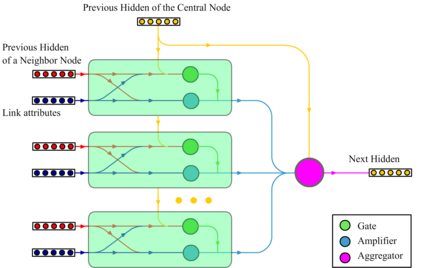
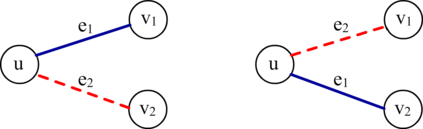
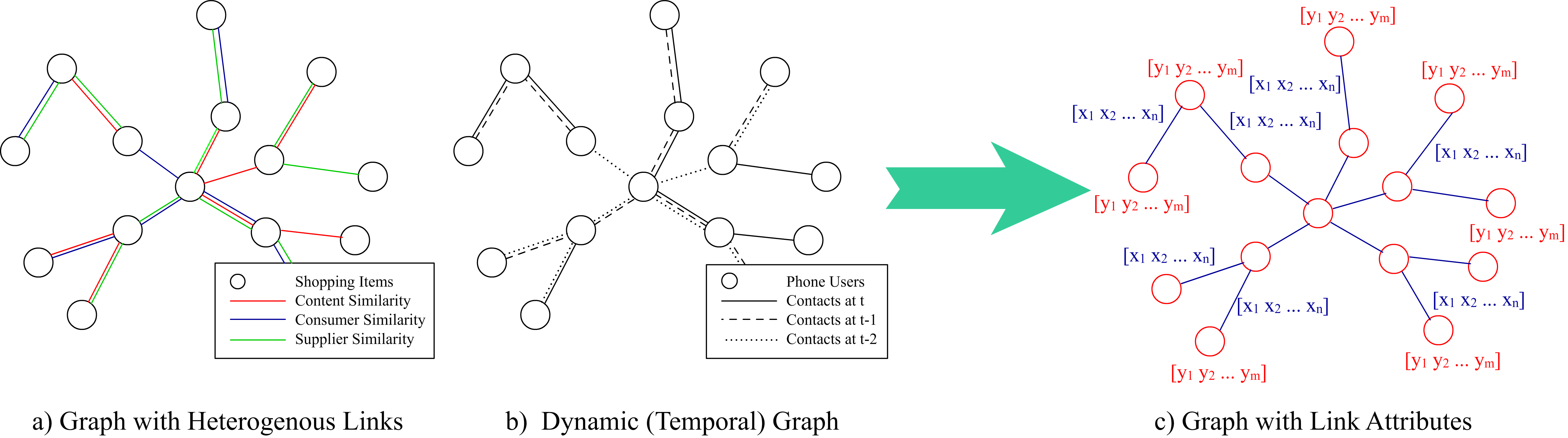
Graph Convolutional Networks (GCNs) have proved to be a most powerful architecture in aggregating local neighborhood information for individual graph nodes. Low-rank proximities and node features are successfully leveraged in existing GCNs, however, attributes that graph links may carry are commonly ignored, as almost all of these models simplify graph links into binary or scalar values describing node connectedness. In our paper instead, links are reverted to hypostatic relationships between entities with descriptional attributes. We propose GCN-LASE (GCN with Link Attributes and Sampling Estimation), a novel GCN model taking both node and link attributes as inputs. To adequately captures the interactions between link and node attributes, their tensor product is used as neighbor features, based on which we define several graph kernels and further develop according architectures for LASE. Besides, to accelerate the training process, the sum of features in entire neighborhoods are estimated through Monte Carlo method, with novel sampling strategies designed for LASE to minimize the estimation variance. Our experiments show that LASE outperforms strong baselines over various graph datasets, and further experiments corroborate the informativeness of link attributes and our model's ability of adequately leveraging them.
翻译:图形相连接网络(GCNs)已被证明是汇集单个图形节点的地方邻居信息的最强大的架构。 在现有GCN中,低级别近似和节点功能被成功利用。 然而,图形链接可能携带的属性通常被忽略,因为几乎所有这些模型都简化了图形链接,进入描述连接节点的二进制或弧值。在我们的文件中,链接被恢复到具有描述属性的实体之间的低等关系。 我们提出了GCN-LASE(带有链接属性和抽样估计的GCN),这是一个新型的GCN模型,同时将节点和节点属性作为投入。为了充分捕捉链接和节点属性之间的相互作用,它们的变色素产品被用作邻居特征,在此基础上我们定义了几个图形内核,并进一步发展了LASE的架构。此外,为了加快培训进程,整个周边特征的总和是通过Monte Carlo方法估算的,为LASE而设计了新的抽样战略,以尽量减少估计差异。我们的实验表明,LASESE超越了各种图表数据属性链接的强大基线。