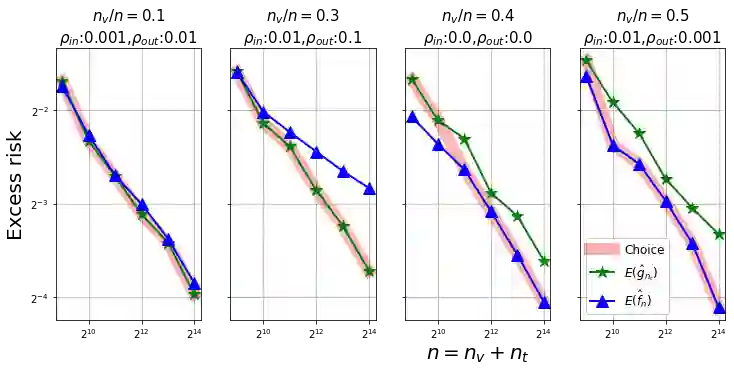
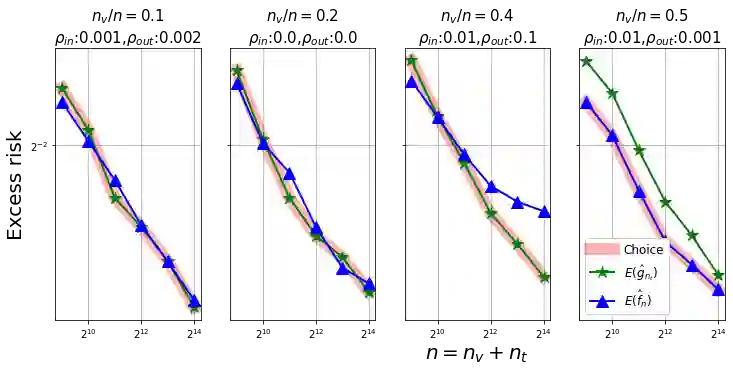
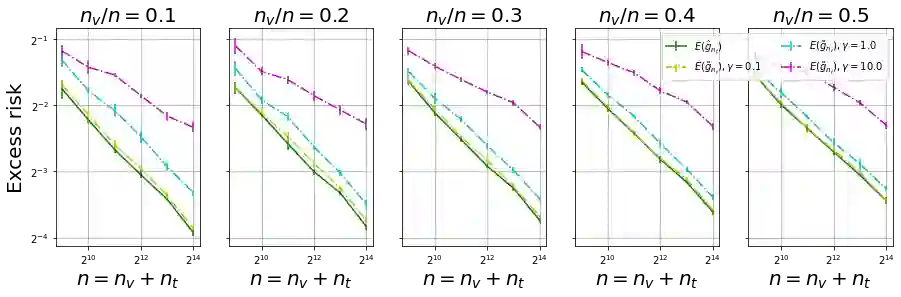
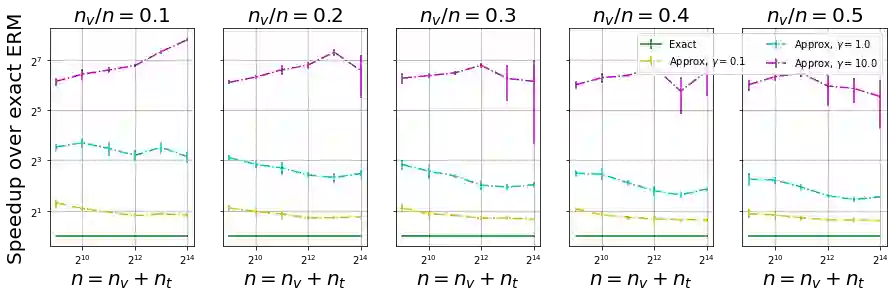
We show, to our knowledge, the first theoretical treatments of two common questions in cross-validation based hyperparameter selection: (1) After selecting the best hyperparameter using a held-out set, we train the final model using {\em all} of the training data -- since this may or may not improve future generalization error, should one do this? (2) During optimization such as via SGD (stochastic gradient descent), we must set the optimization tolerance $\rho$ -- since it trades off predictive accuracy with computation cost, how should one set it? Toward these problems, we introduce the {\em hold-in risk} (the error due to not using the whole training data), and the {\em model class mis-specification risk} (the error due to having chosen the wrong model class) in a theoretical view which is simple, general, and suggests heuristics that can be used when faced with a dataset instance. In proof-of-concept studies in synthetic data where theoretical quantities can be controlled, we show that these heuristics can, respectively, (1) always perform at least as well as always performing retraining or never performing retraining, (2) either improve performance or reduce computational overhead by $2\times$ with no loss in predictive performance.
翻译:据我们所知,在交叉验证基于超参数的选择中,我们展示了对两个共同问题的最初理论处理方法,即交叉校准基于超分计选择最佳超参数之后:(1) 在使用一个搁置的套件选择最佳超参数之后,我们用培训数据中的[所有]来培训最后模型 -- -- 因为这样可能或不会改进未来的概括错误,我们是否应该这样做?(2) 在优化过程中,例如通过SGD(随机梯度梯度下降),我们必须设定优化容忍度$rho$ -- -- 因为它与计算成本的预测准确性相交换,如何设定它?为了解决这些问题,我们引入了`它们持有风险'(由于没有使用整个培训数据造成的错误) 和`它们类模型错误区分风险}(由于选择错误的模型类别),是否应该这样做?(2) 在使用简单、一般的理论观点和暗示在面对数据集时可以使用的超理论实例。在对可控制理论量的合成数据进行有说服力的研究中,我们表明,这些超率可以分别(1) 以美元进行至少进行经常性的再培训或从未进行再培训,或者从不进行高层再分析,至少进行2美元,至少进行两次再培训。