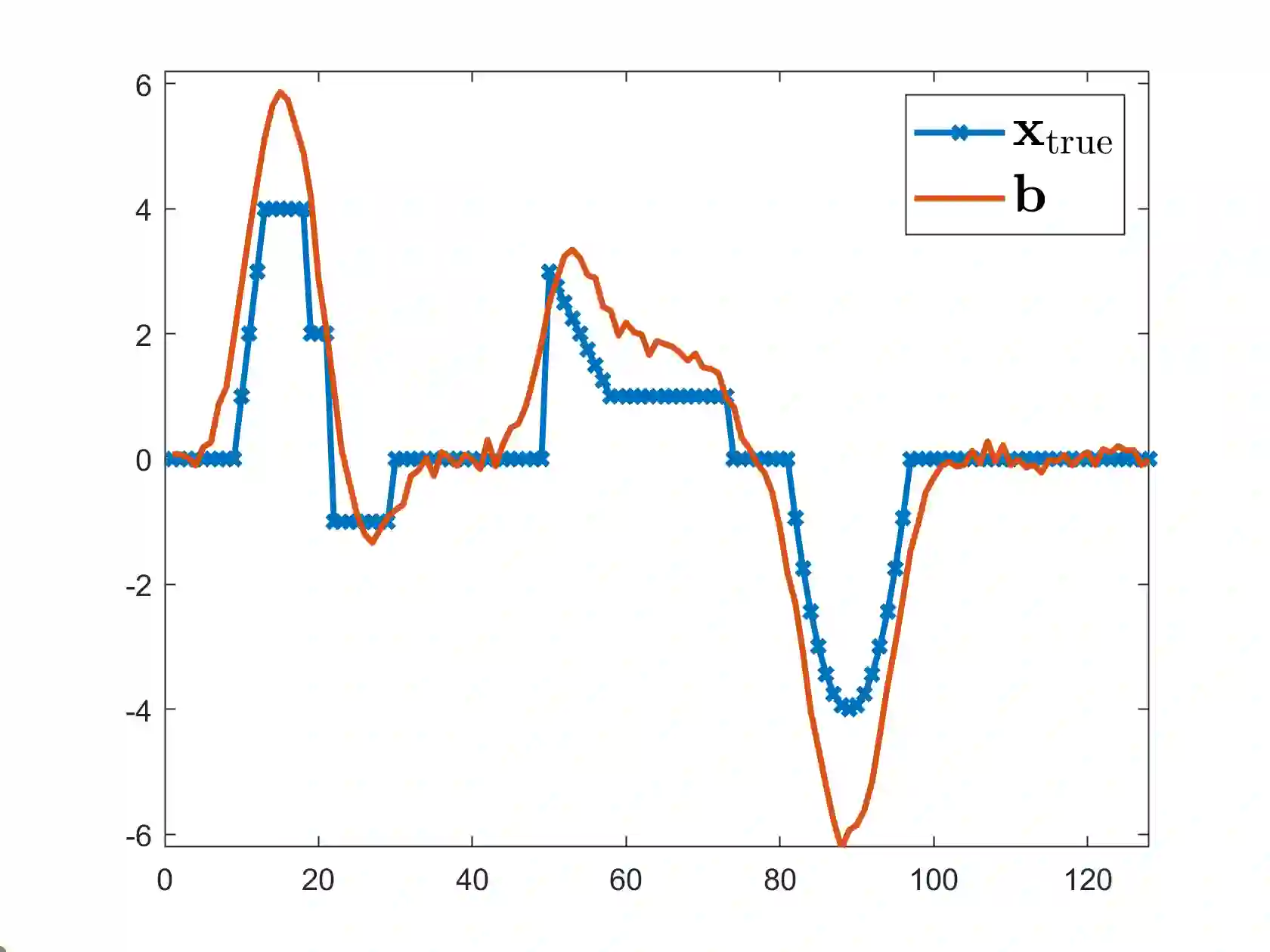
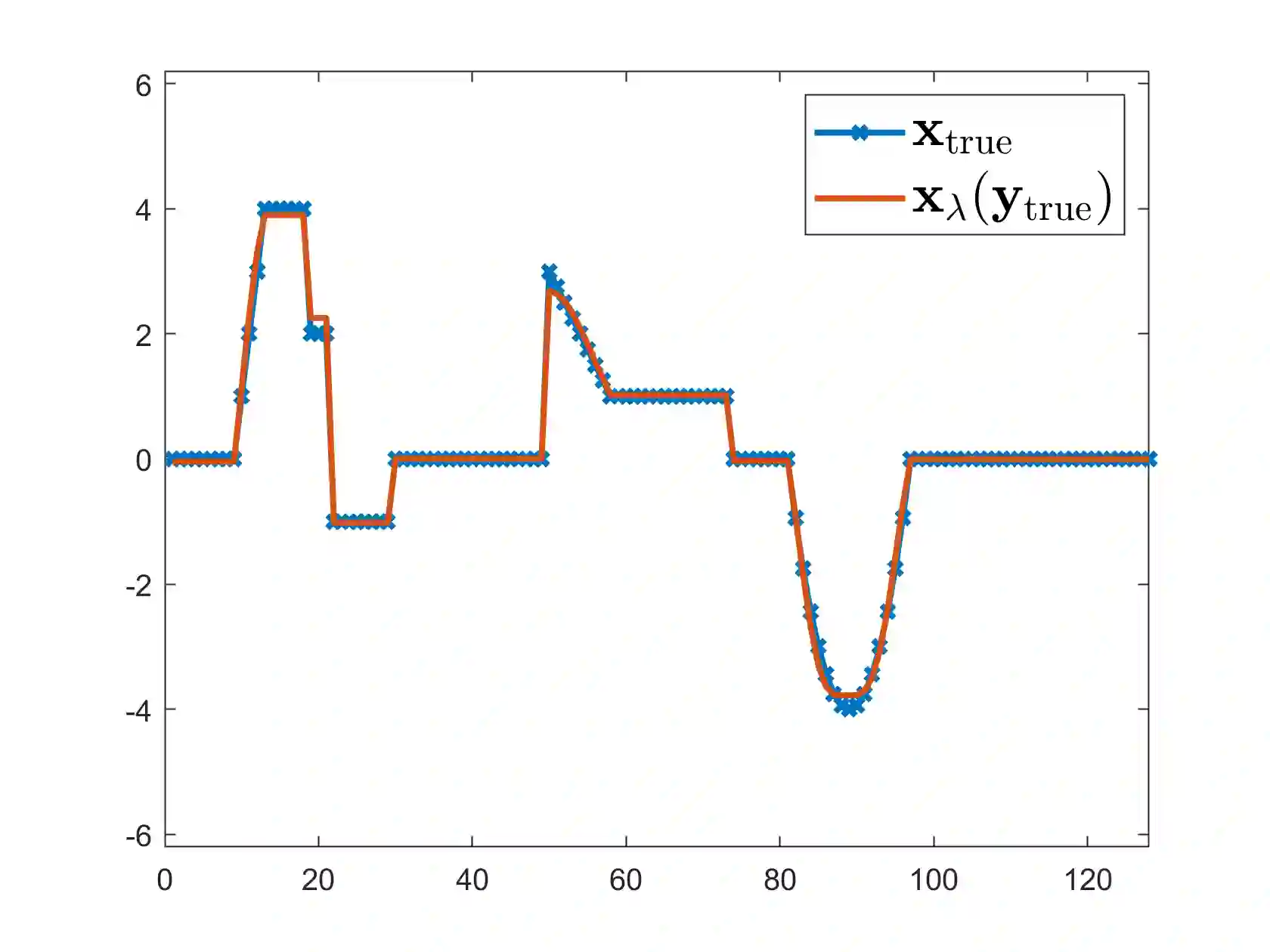
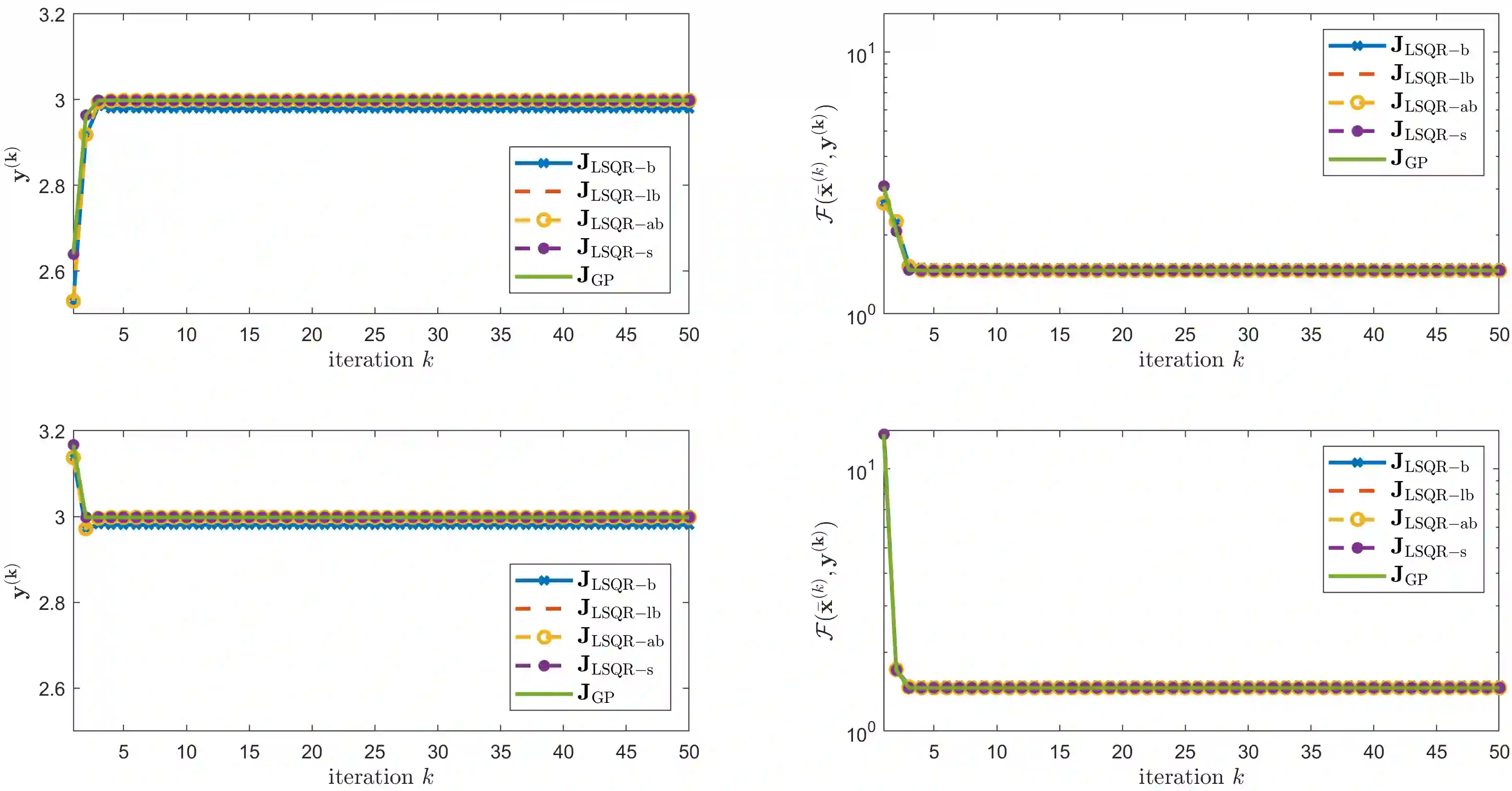
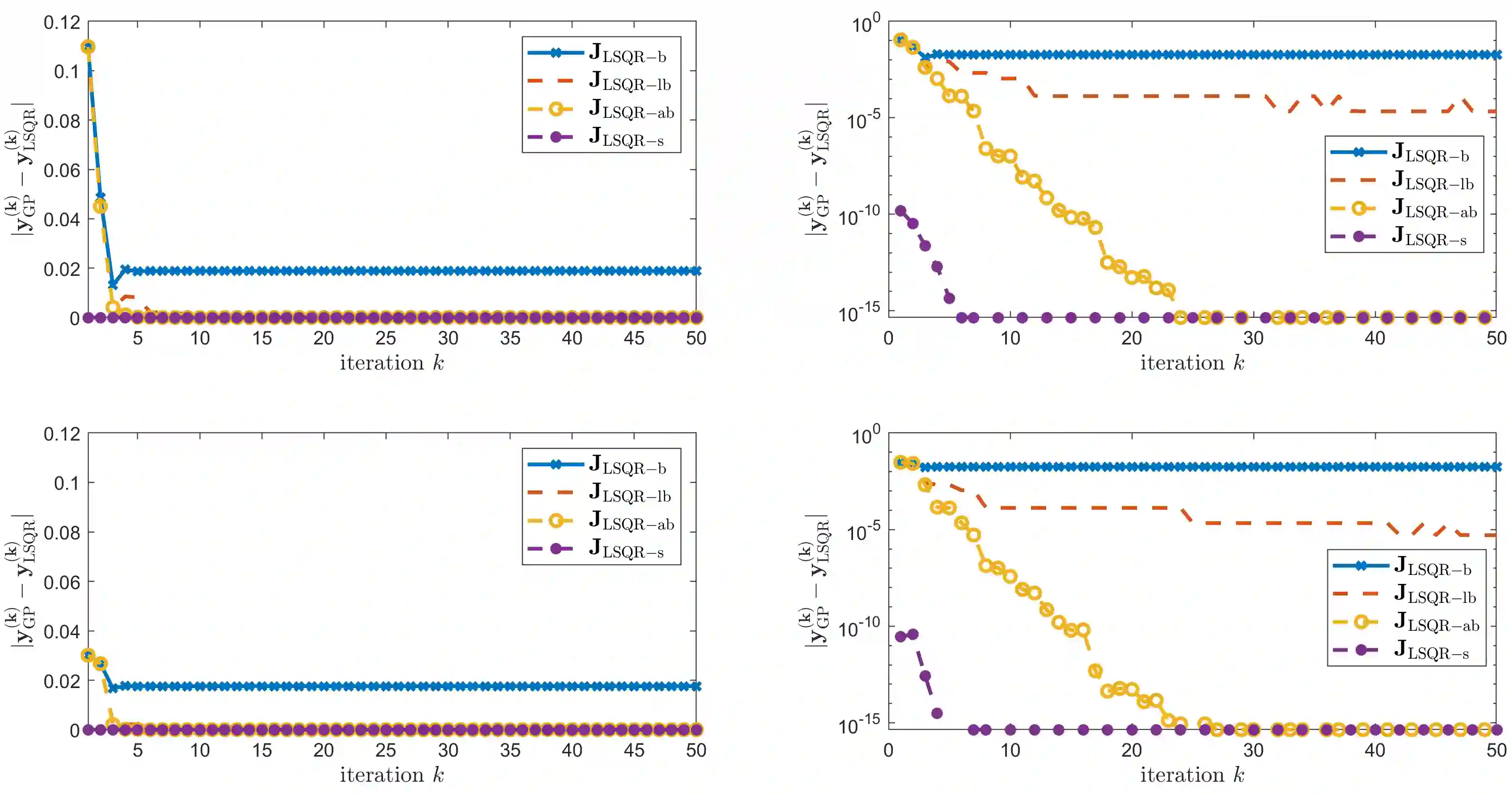
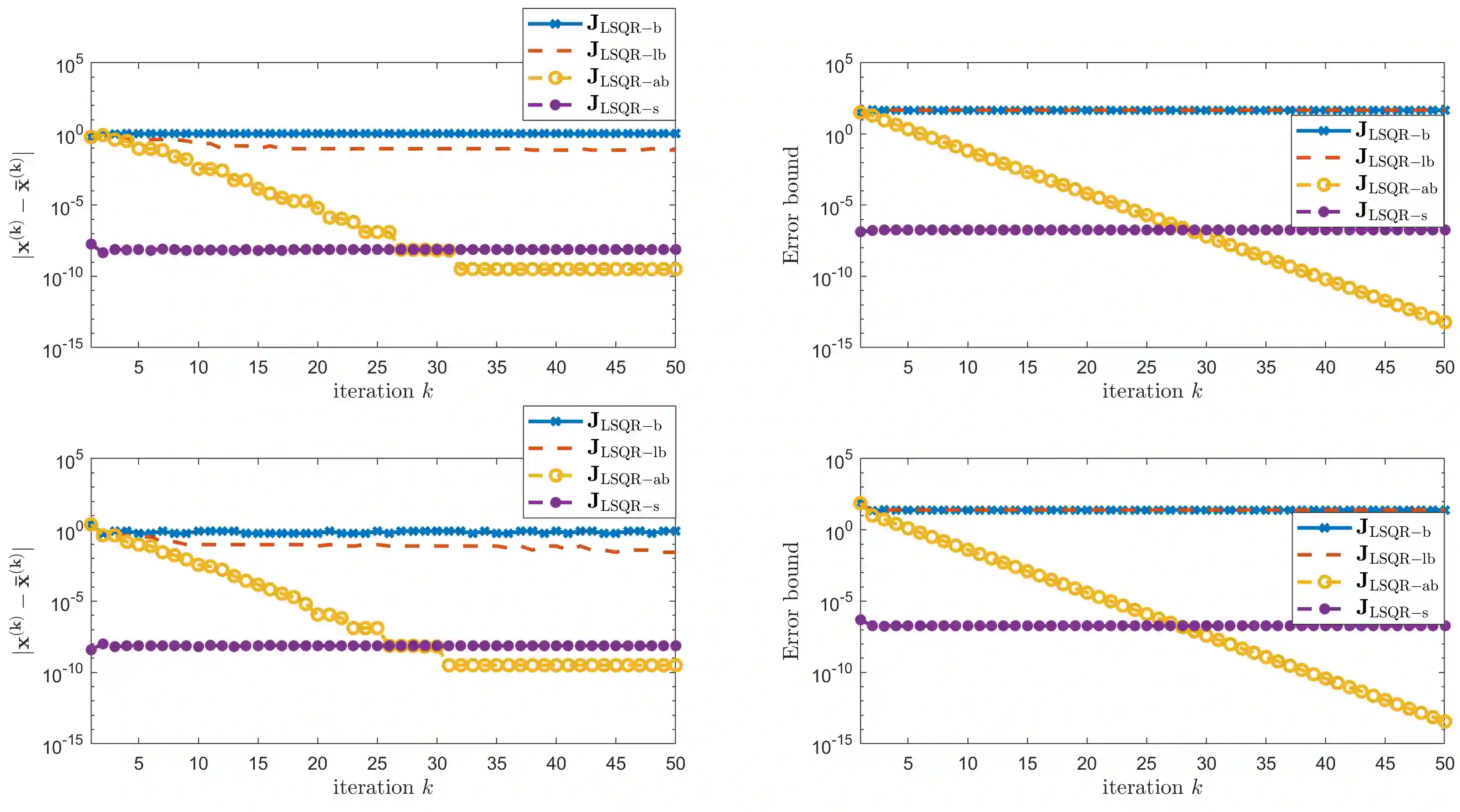
Variable projection methods prove highly efficient in solving separable nonlinear least squares problems by transforming them into a reduced nonlinear least squares problem, typically solvable via the Gauss-Newton method. When solving large-scale separable nonlinear inverse problems with general-form Tikhonov regularization, the computational demand for computing Jacobians in the Gauss-Newton method becomes very challenging. To mitigate this, iterative methods, specifically LSQR, can be used as inner solvers to compute approximate Jacobians. This article analyzes the impact of these approximate Jacobians within the variable projection method and introduces stopping criteria to ensure convergence. We also present numerical experiments where we apply the proposed method to solve a blind deconvolution problem to illustrate and confirm our theoretical results.
翻译:暂无翻译