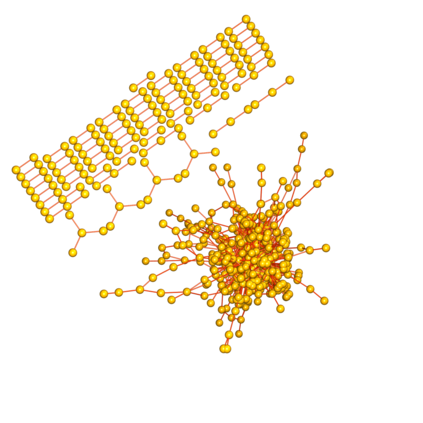
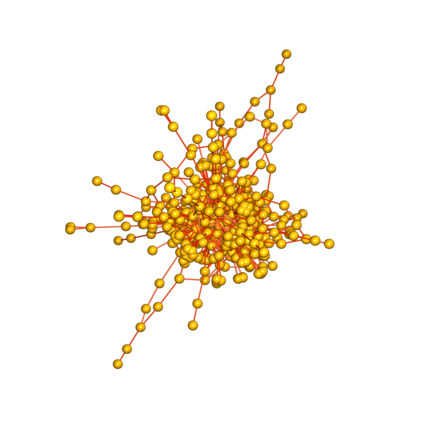
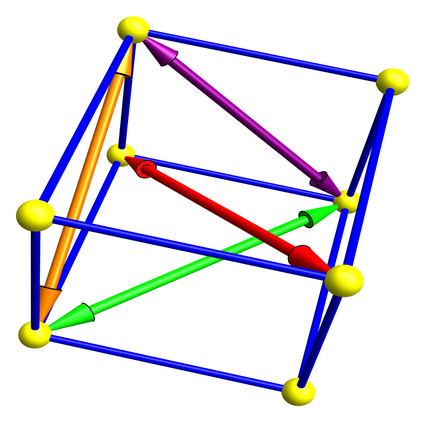
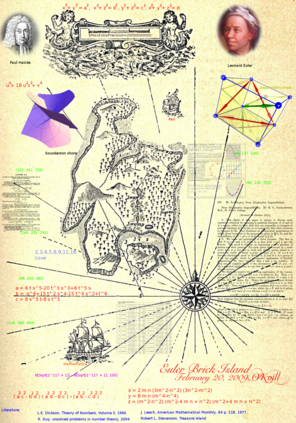
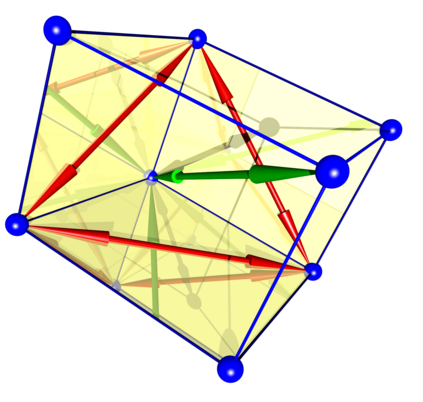
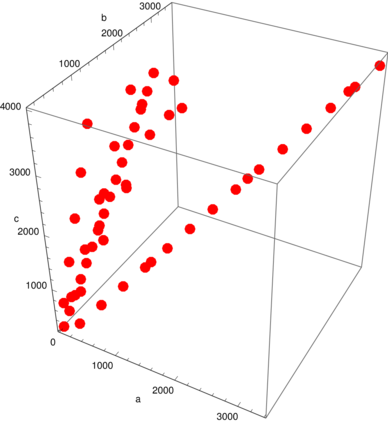
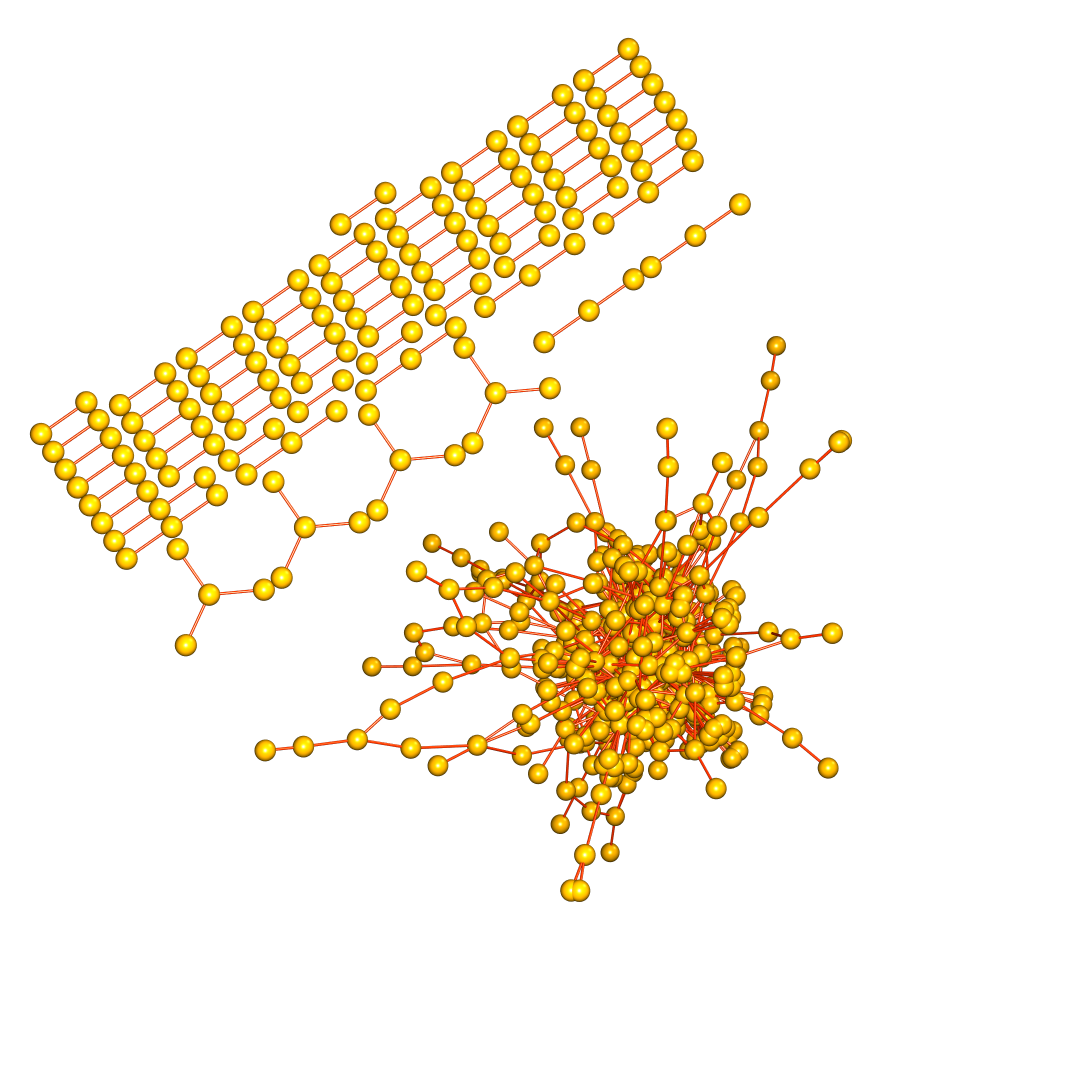
The Babylonian graph B has the positive integers as vertices and connects two if they define a Pythagorean triple. Triangular subgraphs correspond to Euler bricks. What are the properties of this graph? Are there tetrahedral subgraphs corresponding to Euler tesseracts? Is there only one infinite connected component? Are there two Euler bricks in the graph that are disconnected? Do the number of edges or triangles in the subgraph generated by the first n vertices grow like of the order n W(n), where n is the product log? We prove here some first results like the threshold where B(n) becomes non-planar. In an appendix, we include handout from a talk on Euler cuboids given in the year 2009.
翻译：巴比伦图B将正数整数作为顶点, 如果它们定义了 Pythagorean 的三重, 则连接两个。 三角子图对应了 Euler 砖块。 此图的属性是什么? 此图是否具有与 Euler Tesseract 相对应的四面体子图? 是否只有一个无限的连接部件? 图形中是否有两个断开的 Euler 砖? 第一个n 顶点产生的子图中边缘或三角数是否像产品日志n(n) 的顺序那样增长? 我们在这里证明一些初步结果, 比如 B(n) 变成非平面的临界值。 在附录中, 我们包含2009年Euler 幼类演讲的帮助。
相关内容
微信扫码咨询专知VIP会员