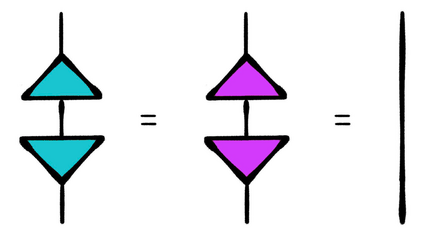
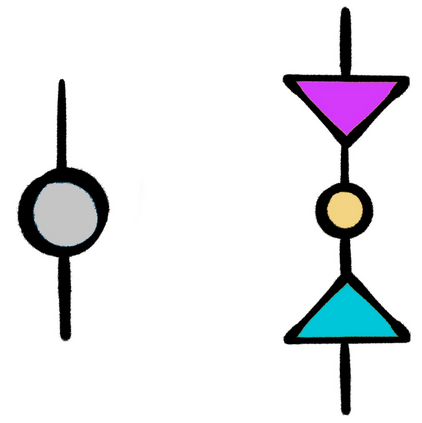
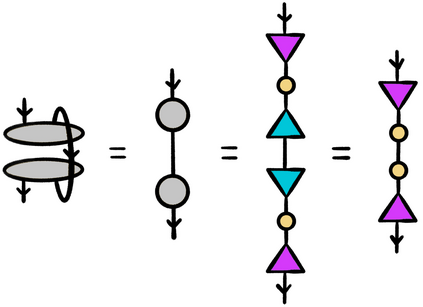
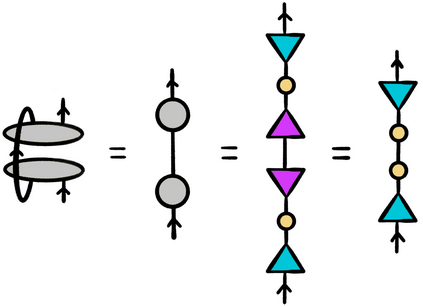
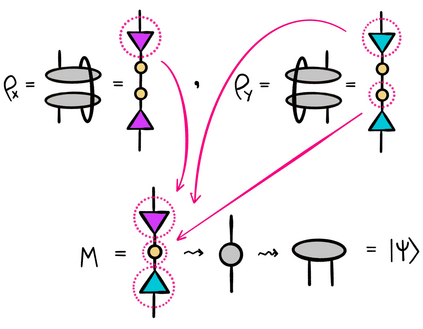
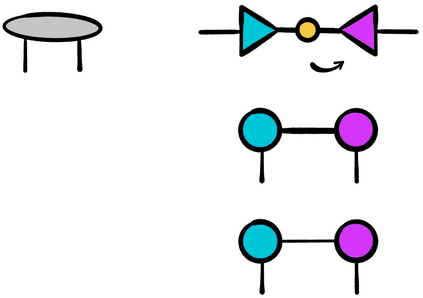
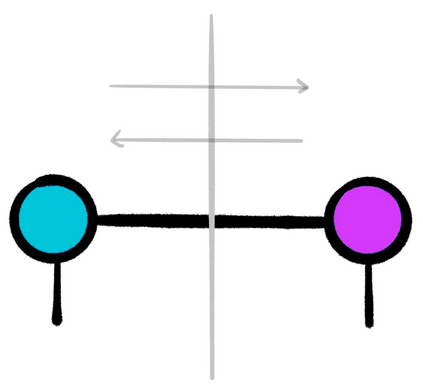
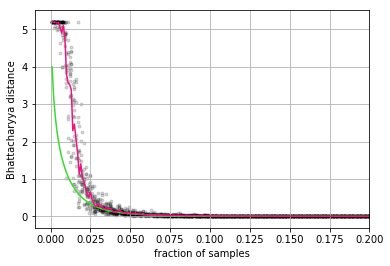
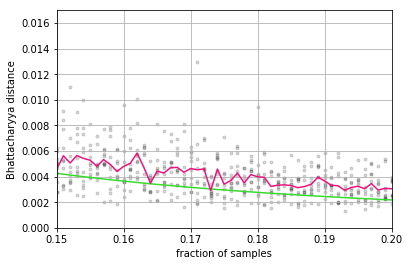
This thesis takes inspiration from quantum physics to investigate mathematical structure that lies at the interface of algebra and statistics. The starting point is a passage from classical probability theory to quantum probability theory. The quantum version of a probability distribution is a density operator, the quantum version of marginalizing is an operation called the partial trace, and the quantum version of a marginal probability distribution is a reduced density operator. Every joint probability distribution on a finite set can be modeled as a rank one density operator. By applying the partial trace, we obtain reduced density operators whose diagonals recover classical marginal probabilities. In general, these reduced densities will have rank higher than one, and their eigenvalues and eigenvectors will contain extra information that encodes subsystem interactions governed by statistics. We decode this information, and show it is akin to conditional probability, and then investigate the extent to which the eigenvectors capture "concepts" inherent in the original joint distribution. The theory is then illustrated with an experiment that exploits these ideas. Turning to a more theoretical application, we also discuss a preliminary framework for modeling entailment and concept hierarchy in natural language, namely, by representing expressions in the language as densities. Finally, initial inspiration for this thesis comes from formal concept analysis, which finds many striking parallels with the linear algebra. The parallels are not coincidental, and a common blueprint is found in category theory. We close with an exposition on free (co)completions and how the free-forgetful adjunctions in which they arise strongly suggest that in certain categorical contexts, the "fixed points" of a morphism with its adjoint encode interesting information.
翻译:从量子物理中提取灵感, 用于调查位于代数和统计界面的数学结构。 起点是从古典概率理论到量子概率理论的一段段落。 概率分布的量子版本是一个密度运算器, 边际分布的量子版本是一个叫做部分跟踪的操作, 边际概率分布的量子版本是一个降低密度运算器。 限数组的每个联合概率分布都可以建模成一个级密度操作器。 通过应用部分跟踪, 我们获得了密度减少的操作器, 其二进制恢复了经典边缘概率。 一般来说, 这些衰减的密度将比一个位高, 其偏差值和量概率分配的量分配器将包含额外的信息, 编码受统计制约的子系互动的量的量分量版本是一个叫做部分跟踪, 而边际分布的量分配的量是最小值分配。 然后通过一个实验来解释这些理论的精度。 理论会用一个更理论应用程序, 我们还会讨论一个预的架构框架, 将它作为直径的直径直值的直径直线论, 。