A Deep Learning approach to Reduced Order Modelling of Parameter Dependent Partial Differential Equations

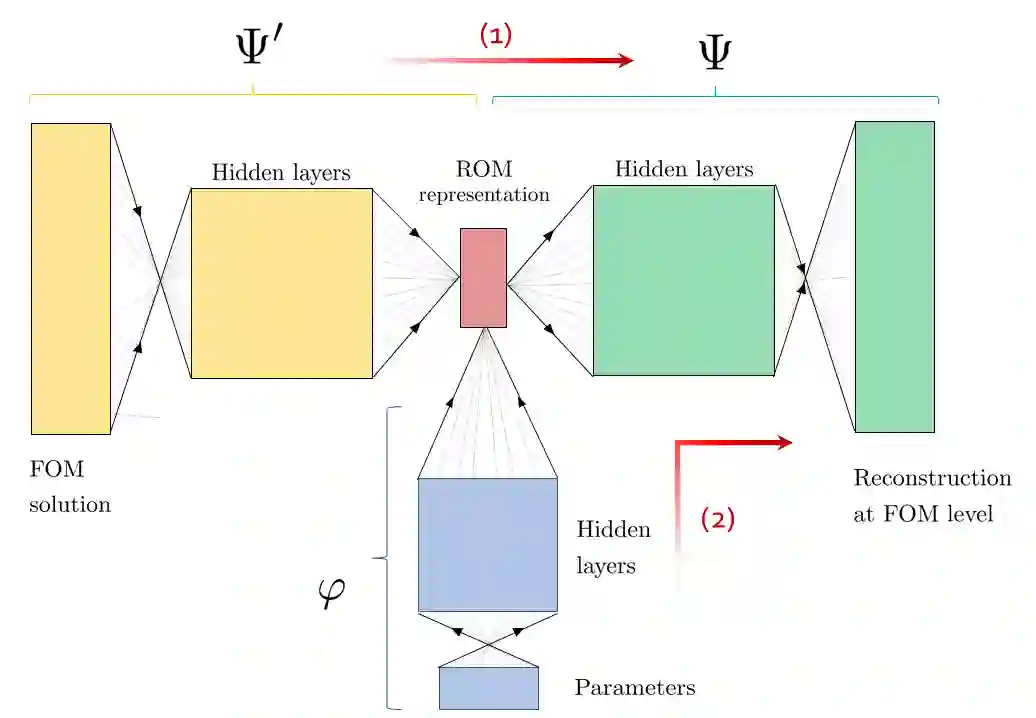
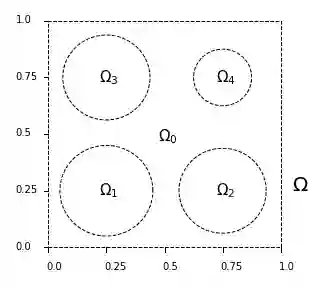
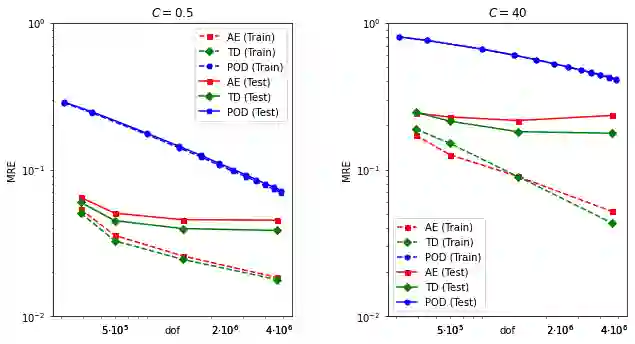
Within the framework of parameter dependent PDEs, we develop a constructive approach based on Deep Neural Networks for the efficient approximation of the parameter-to-solution map. The research is motivated by the limitations and drawbacks of state-of-the-art algorithms, such as the Reduced Basis method, when addressing problems that show a slow decay in the Kolmogorov n-width. Our work is based on the use of deep autoencoders, which we employ for encoding and decoding a high fidelity approximation of the solution manifold. In order to fully exploit the approximation capabilities of neural networks, we consider a nonlinear version of the Kolmogorov n-width over which we base the concept of a minimal latent dimension. We show that this minimal dimension is intimately related to the topological properties of the solution manifold, and we provide some theoretical results with particular emphasis on second order elliptic PDEs. Finally, we report numerical experiments where we compare the proposed approach with classical POD-Galerkin reduced order models. In particular, we consider parametrized advection-diffusion PDEs, and we test the methodology in the presence of strong transport fields, singular terms and stochastic coefficients.