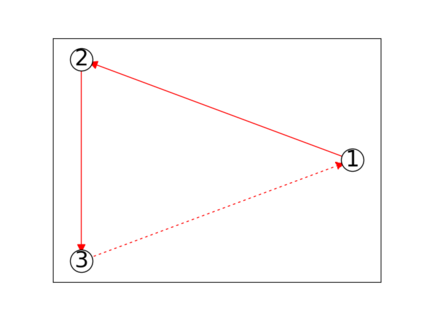
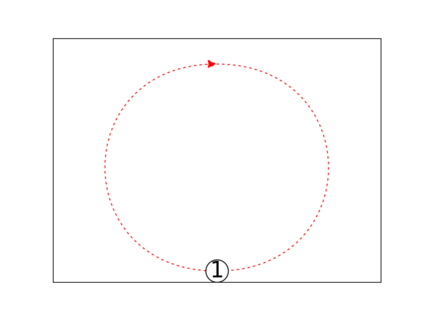
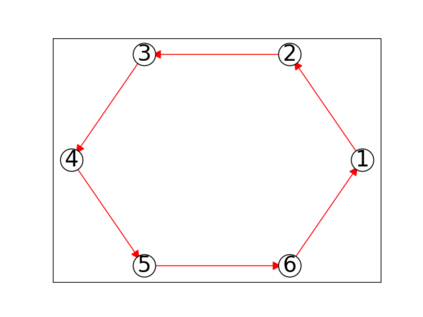
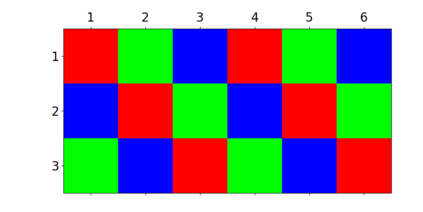
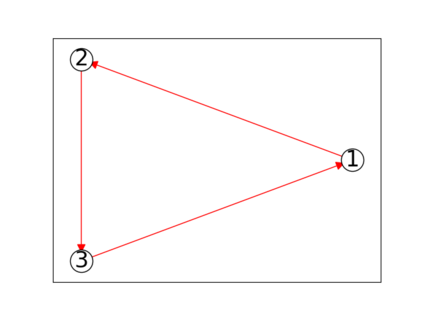
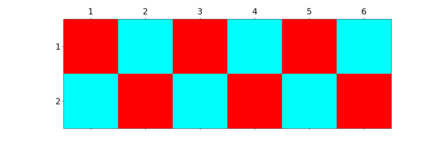
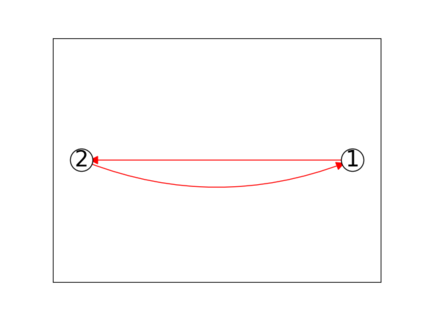
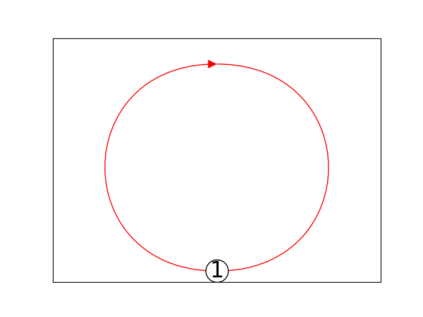
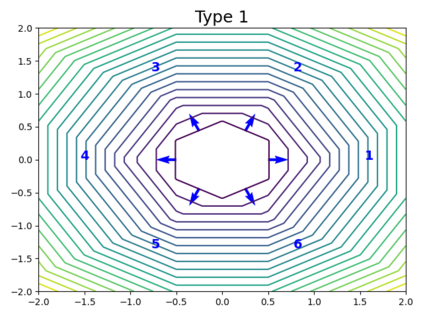
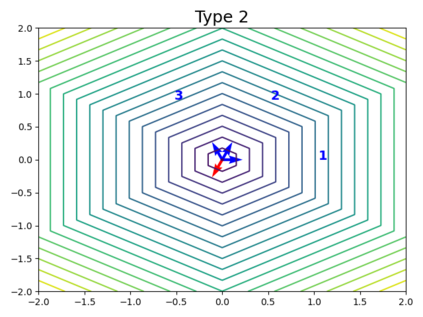
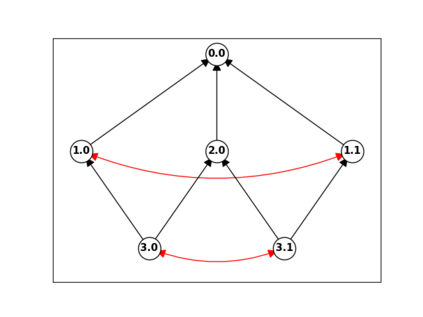
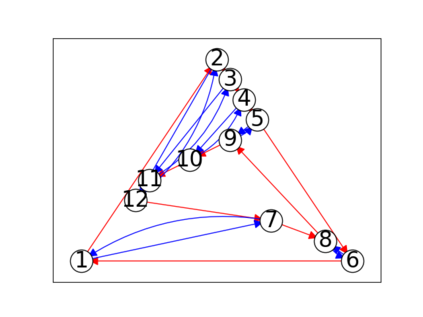
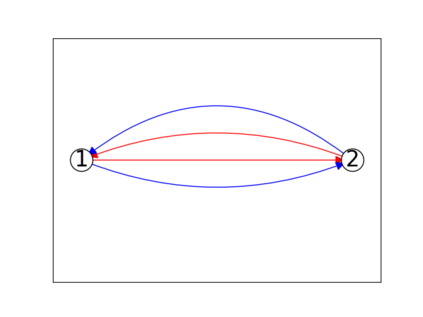
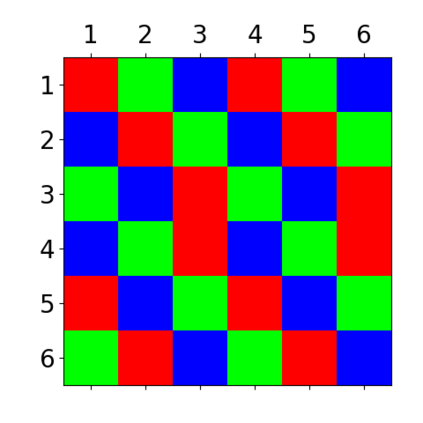
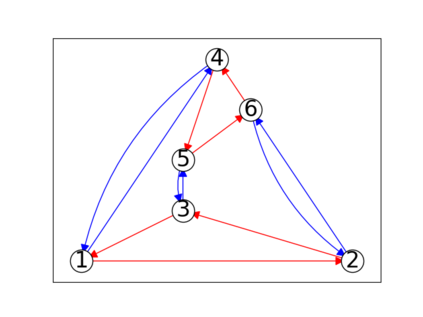
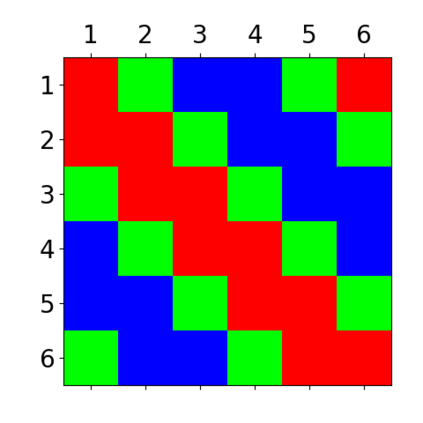
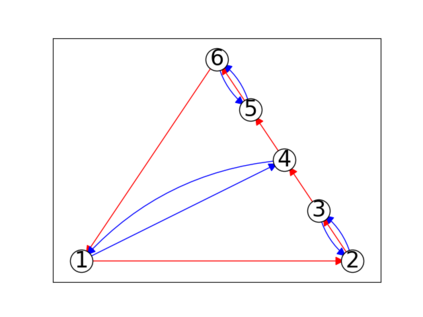
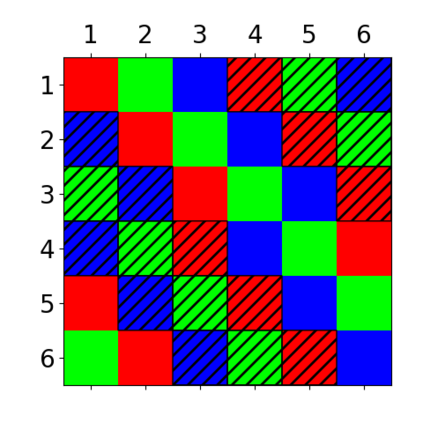
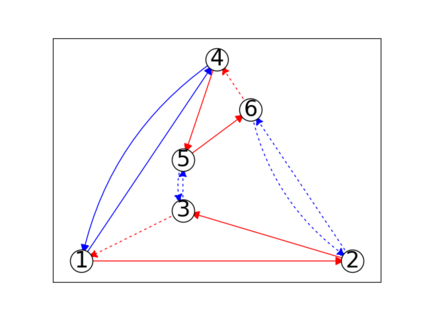
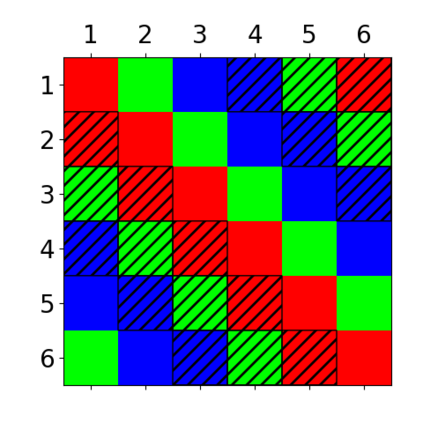
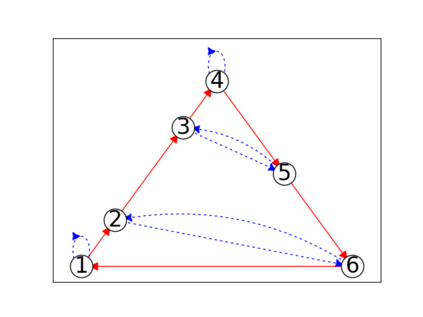
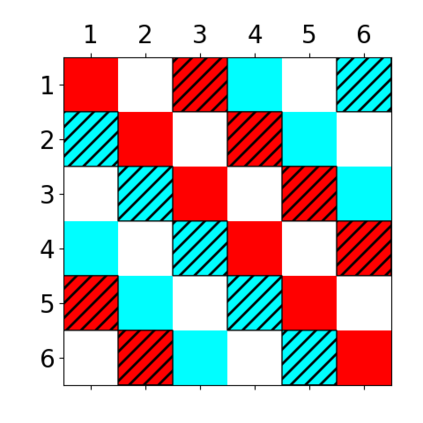
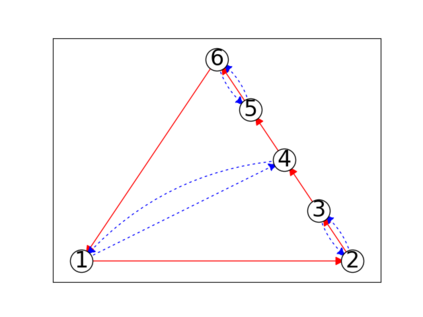
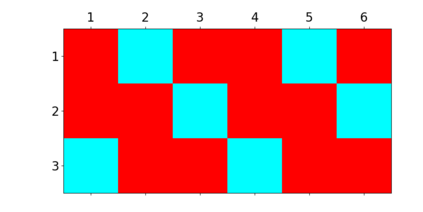
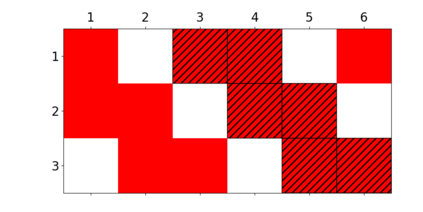
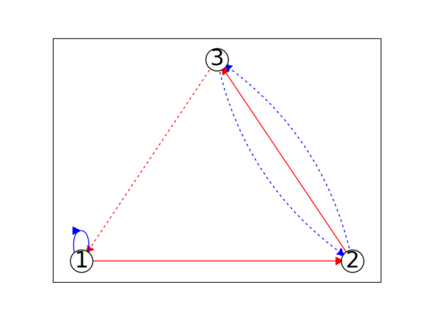
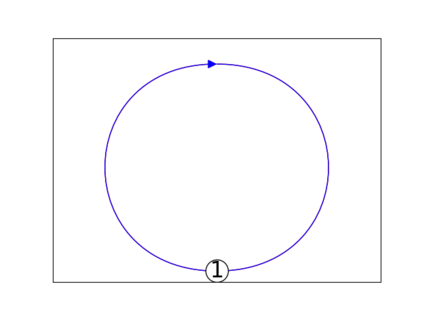
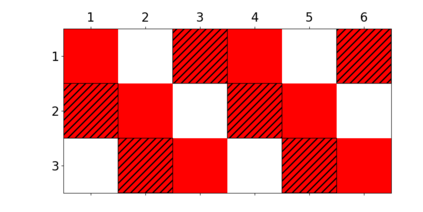
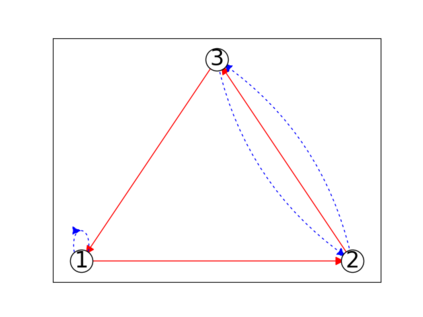
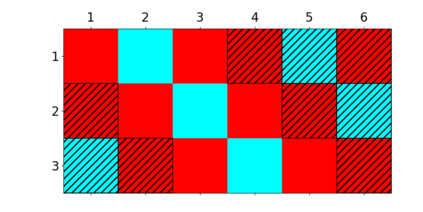
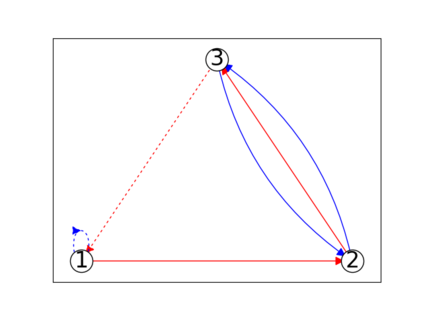
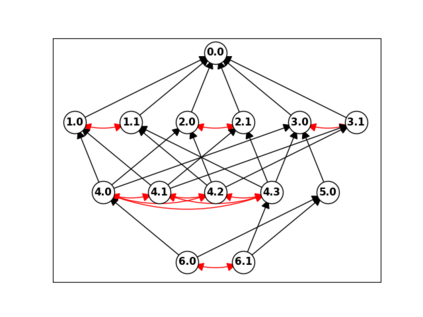
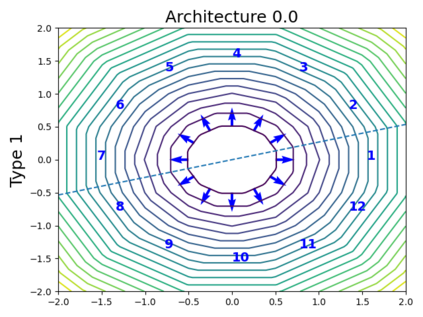
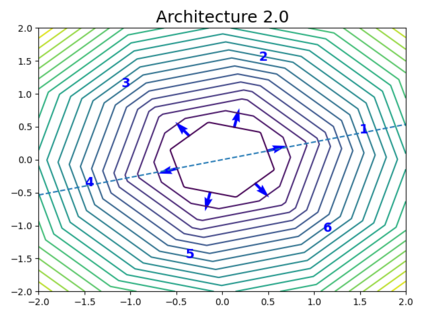
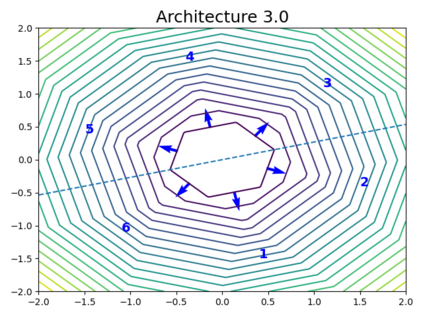
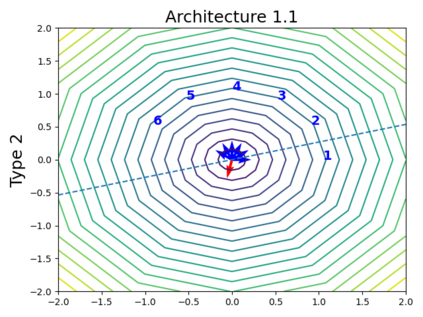
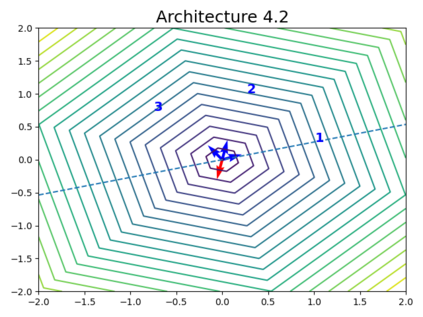
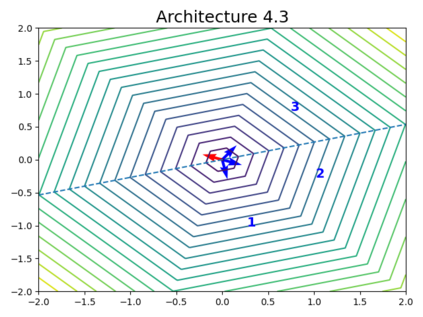
When trying to fit a deep neural network (DNN) to a $G$-invariant target function with respect to a group $G$, it only makes sense to constrain the DNN to be $G$-invariant as well. However, there can be many different ways to do this, thus raising the problem of "$G$-invariant neural architecture design": What is the optimal $G$-invariant architecture for a given problem? Before we can consider the optimization problem itself, we must understand the search space, the architectures in it, and how they relate to one another. In this paper, we take a first step towards this goal; we prove a theorem that gives a classification of all $G$-invariant single-hidden-layer or "shallow" neural network ($G$-SNN) architectures with ReLU activation for any finite orthogonal group $G$. The proof is based on a correspondence of every $G$-SNN to a signed permutation representation of $G$ acting on the hidden neurons. The classification is equivalently given in terms of the first cohomology classes of $G$, thus admitting a topological interpretation. Based on a code implementation, we enumerate the $G$-SNN architectures for some example groups $G$ and visualize their structure. We draw the network morphisms between the enumerated architectures that can be leveraged during neural architecture search (NAS). Finally, we prove that architectures corresponding to inequivalent cohomology classes in a given cohomology ring coincide in function space only when their weight matrices are zero, and we discuss the implications of this in the context of NAS.
翻译:当试图将深层神经网络(DNN) 与一个组的 G$- 变化中目标功能相匹配时, 将DNN 限制为 G$- 变化中。 当试图将深层神经网络(DNN) 与一个组的 G$- 变化中目标函数相匹配时, 将DNN 限制为 G$- 变化中。 但是, 这样做可能有许多不同的方式, 从而提出了“ G$- 变化中神经结构设计 ” 的问题 : 对于某个特定的问题, 什么是最佳的 $- 变化中结构? 在我们考虑优化问题本身之前, 我们必须理解搜索空间、 其中的结构以及它们与另一组的关系。 在本文中, 我们迈出了第一步, 我们证明了一个Oal- 变化中的所有G$- 变化中的数据结构的分类, 也就是我们头层结构的排序, 也就是我们头层结构的排序, 也就是我们头层结构的排序, 也就是我们头层结构的排序, 。