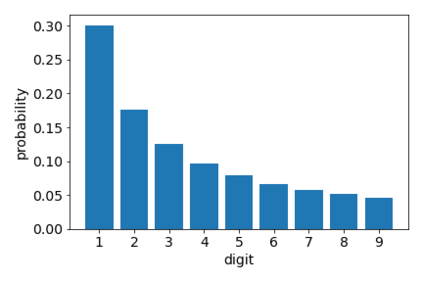
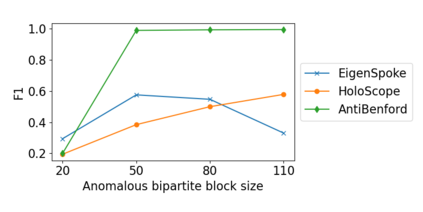
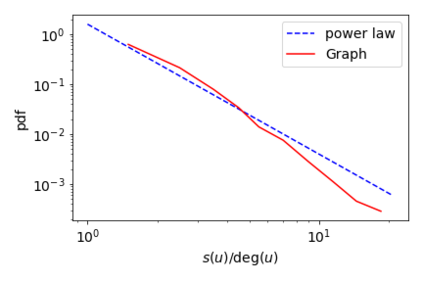
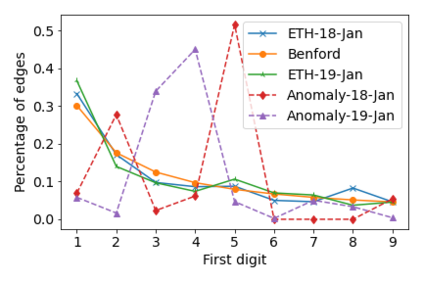
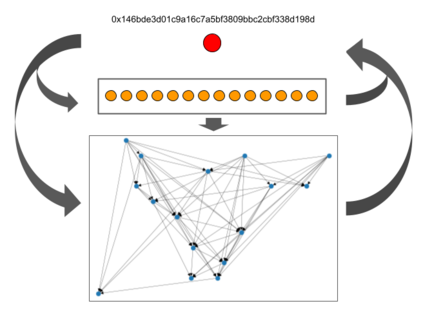
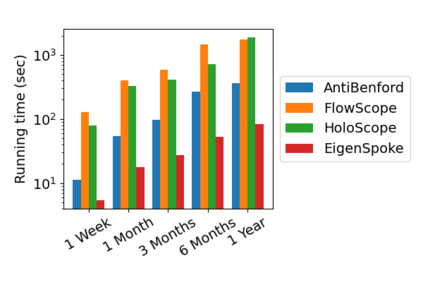
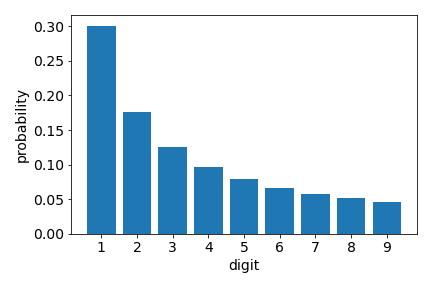
Benford's law describes the distribution of the first digit of numbers appearing in a wide variety of numerical data, including tax records, and election outcomes, and has been used to raise "red flags" about potential anomalies in the data such as tax evasion. In this work, we ask the following novel question: given a large transaction or financial graph, how do we find a set of nodes that perform many transactions among each other that also deviate significantly from Benford's law? We propose the AntiBenford subgraph framework that is founded on well-established statistical principles. Furthermore, we design an efficient algorithm that finds AntiBenford subgraphs in near-linear time on real data. We evaluate our framework on both real and synthetic data against a variety of competitors. We show empirically that our proposed framework enables the detection of anomalous subgraphs in cryptocurrency transaction networks that go undetected by state-of-the-art graph-based anomaly detection methods. Our empirical findings show that our \ab framework is able to mine anomalous subgraphs, and provide novel insights into financial transaction data. The code and the datasets are available at \url{https://github.com/tsourakakis-lab/antibenford-subgraphs}.
翻译:Benford 的法律描述了大量数字数据(包括税收记录)和选举结果中数字头数的分布情况,并被用来提高“红旗”“红旗”关于逃税等数据中潜在异常现象的“红旗”。在这项工作中,我们提出以下新颖的问题:考虑到一个巨大的交易或金融图表,我们如何找到一组节点,在彼此之间进行许多交易,而这些交易也与Benford法律大相径庭?我们建议了建立在既定统计原则基础上的反本福分图框架。此外,我们设计了一个高效的算法,在近线时间发现AntiBenford子图,并针对各种竞争者评估我们关于真实和合成数据的框架。我们从经验上表明,我们提议的框架有助于在隐性货币交易网络中检测出无法被基于州艺术的图表的异常检测方法发现的异常现象。我们的实证结果显示,我们的框架能够对异常现象子图进行勘测,并对金融交易数据提供新的洞察。我们的代码和数据可在http://babursqours。