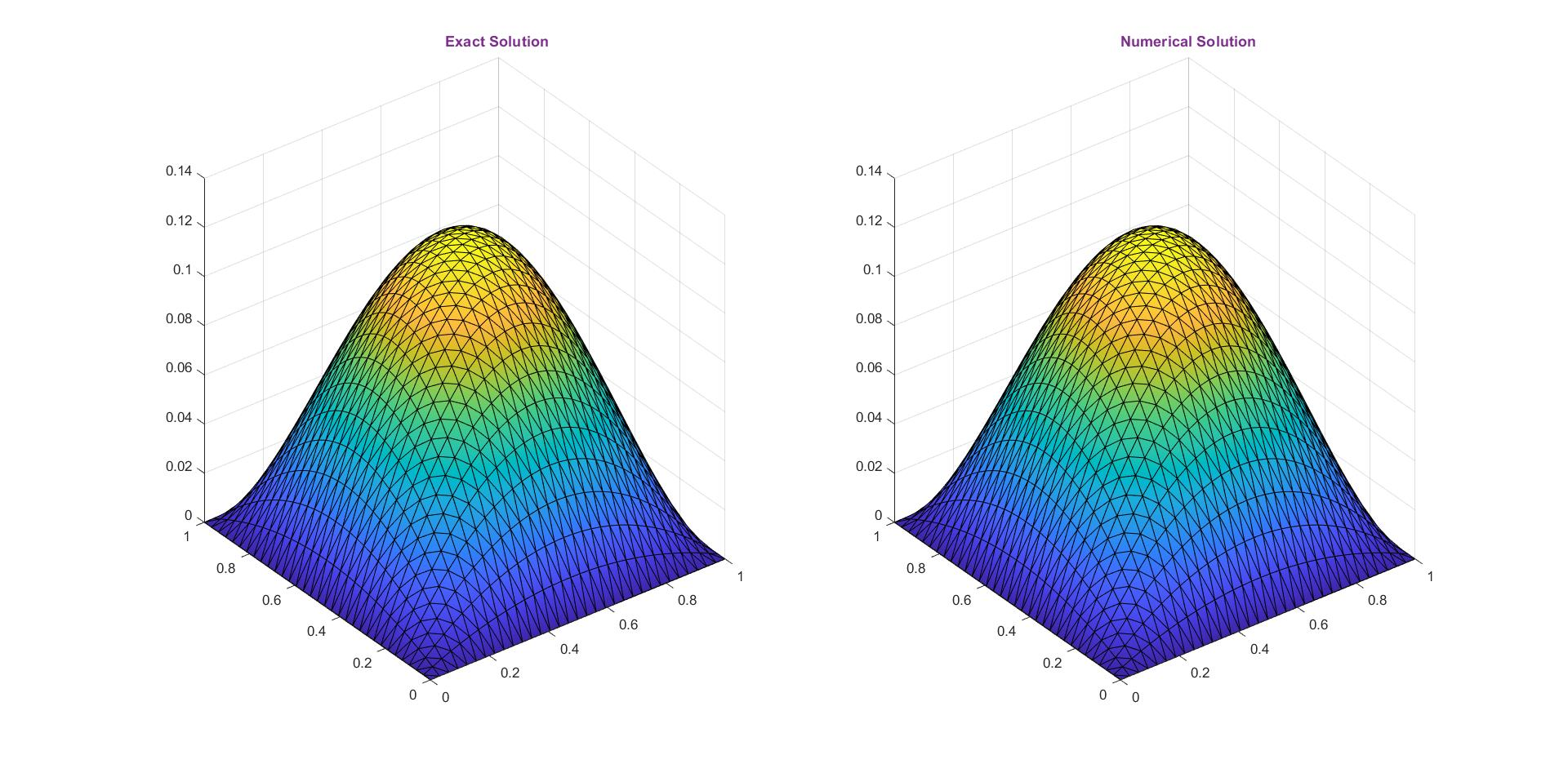
The solution of time fractional partial differential equations in general exhibit a weak singularity near the initial time. In this article we propose a method for solving time fractional diffusion equation with nonlocal diffusion term. The proposed method comprises L1 scheme on graded mesh, finite element method and Newton's method. We discuss the well-posedness of the weak formulation at discrete level and derive \emph{a priori} error estimates for fully-discrete formulation in $L^2(\Omega)$ and $H^1(\Omega)$ norms. Finally, some numerical experiments are conducted to validate the theoretical findings.
翻译:时间分数部分差分方程式的解决方案一般在初始时间附近表现出微弱的单一性。在本条中,我们提出了一个用非局部扩散术语解决时间分数扩散方程式的方法。拟议方法包括分级网格、有限元素法和牛顿法的L1方案。我们讨论了离散层微弱配方的稳妥性,并用$L2(Omega)$和$H1(\Omega)$的规范得出了全分数配方的误差估计数。最后,我们进行了一些数字实验,以验证理论结论。