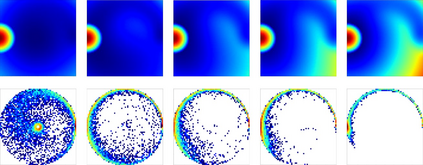
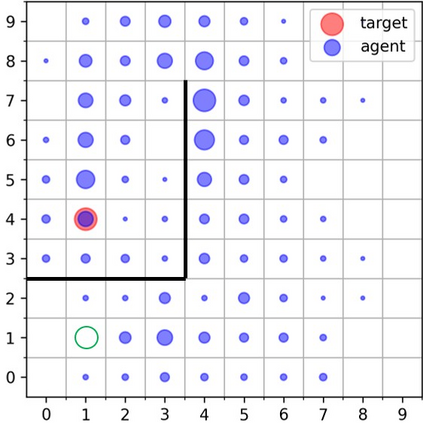
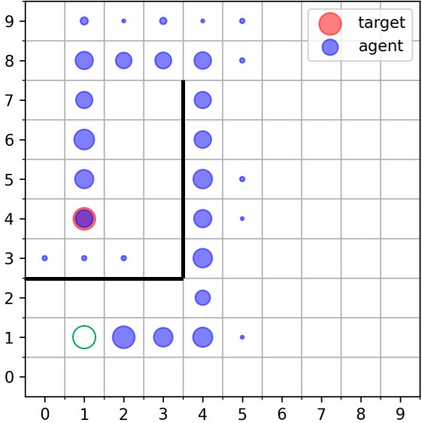
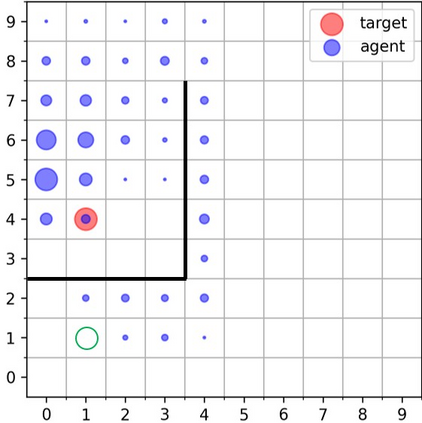
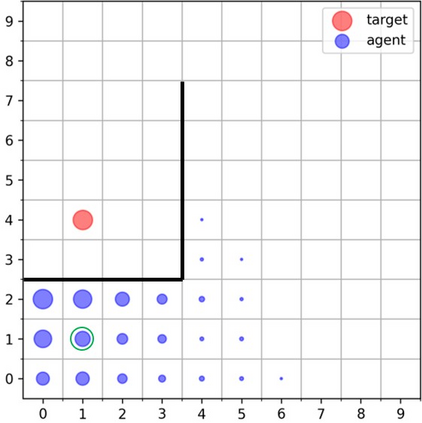
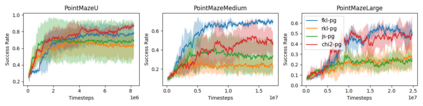
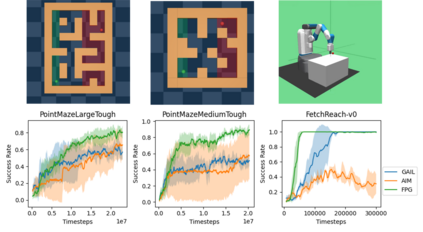
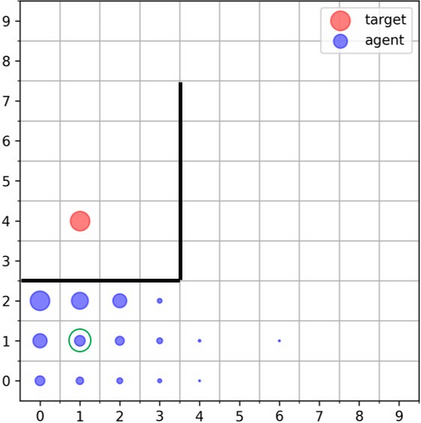
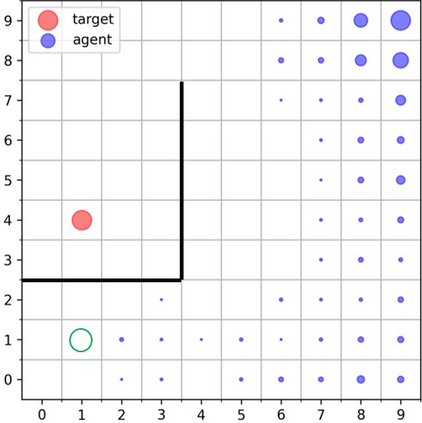
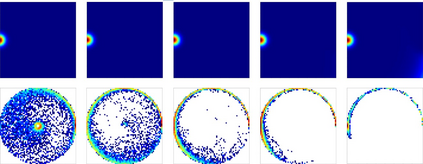
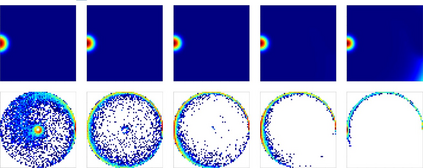
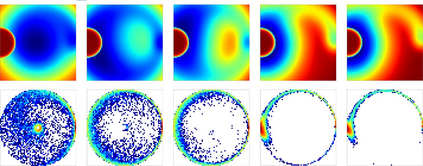
Goal-Conditioned Reinforcement Learning (RL) problems often have access to sparse rewards where the agent receives a reward signal only when it has achieved the goal, making policy optimization a difficult problem. Several works augment this sparse reward with a learned dense reward function, but this can lead to sub-optimal policies if the reward is misaligned. Moreover, recent works have demonstrated that effective shaping rewards for a particular problem can depend on the underlying learning algorithm. This paper introduces a novel way to encourage exploration called $f$-Policy Gradients, or $f$-PG. $f$-PG minimizes the f-divergence between the agent's state visitation distribution and the goal, which we show can lead to an optimal policy. We derive gradients for various f-divergences to optimize this objective. Our learning paradigm provides dense learning signals for exploration in sparse reward settings. We further introduce an entropy-regularized policy optimization objective, that we call $state$-MaxEnt RL (or $s$-MaxEnt RL) as a special case of our objective. We show that several metric-based shaping rewards like L2 can be used with $s$-MaxEnt RL, providing a common ground to study such metric-based shaping rewards with efficient exploration. We find that $f$-PG has better performance compared to standard policy gradient methods on a challenging gridworld as well as the Point Maze and FetchReach environments. More information on our website https://agarwalsiddhant10.github.io/projects/fpg.html.
翻译:暂无翻译