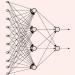
In this work, we present and study Continuous Generative Neural Networks (CGNNs), namely, generative models in the continuous setting: the output of a CGNN belongs to an infinite-dimensional function space. The architecture is inspired by DCGAN, with one fully connected layer, several convolutional layers and nonlinear activation functions. In the continuous $L^2$ setting, the dimensions of the spaces of each layer are replaced by the scales of a multiresolution analysis of a compactly supported wavelet. We present conditions on the convolutional filters and on the nonlinearity that guarantee that a CGNN is injective. This theory finds applications to inverse problems, and allows for deriving Lipschitz stability estimates for (possibly nonlinear) infinite-dimensional inverse problems with unknowns belonging to the manifold generated by a CGNN. Several numerical simulations, including signal deblurring, illustrate and validate this approach.
翻译:在这项研究中,我们提出并研究了连续性生成神经网络(CGNNs),即连续场景下的生成模型:CGNN的输出属于一个无限维的函数空间。CGNN的架构受到DCGAN的启发,其中包括一个全连接层、几个卷积层和非线性激活函数。在连续的$L^2$场景中,每层的空间维度被紧凑支持小波的多分辨率分析的尺度替换。我们提出了对于卷积滤波器和非线性激活函数的条件,以保证CGNN是可逆的。这一理论对于反问题具有应用价值,并允许推导出CGNN生成的流形上的未知数量的(可能非线性)无限维反问题的Lipschitz稳定性估计。包括信号去模糊在内的几个数值模拟,证明了这种方法的可行性。