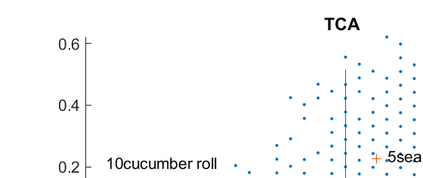
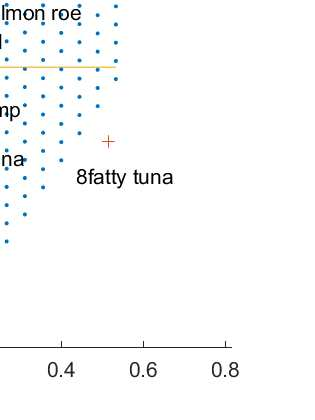
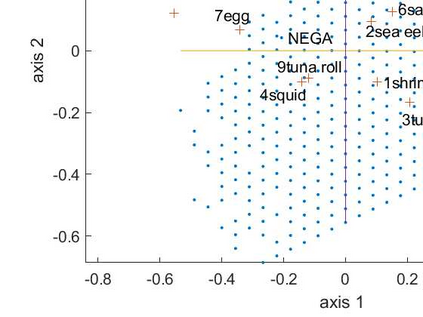
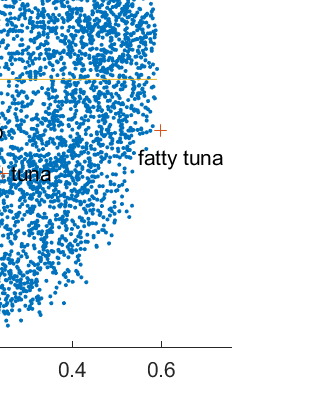
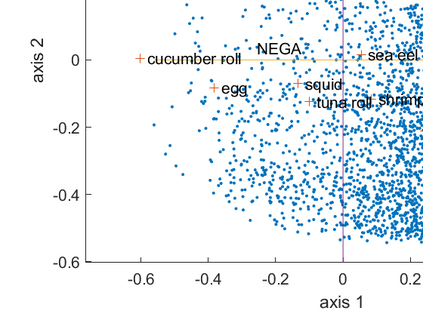
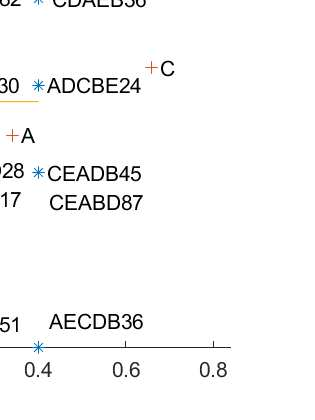
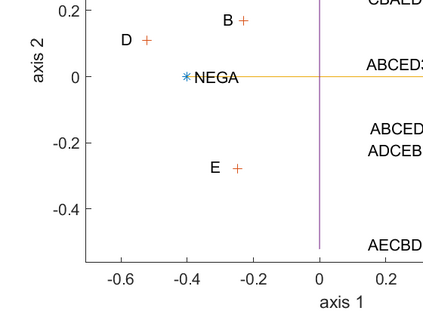
Let n respondents rank order d items, and suppose that d << n. Our main task is to uncover and display the structure of the observed rank data by an exploratory riffle shuffling procedure which sequentially decomposes the n voters into a finite number of coherent groups plus a noisy group : where the noisy group represents the outlier voters and each coherent group is composed of a finite number of coherent clusters. We consider exploratory riffle shuffling of a set of items to be equivalent to optimal two blocks seriation of the items with crossing of some scores between the two blocks. A riffle shuffled coherent cluster of voters within its coherent group is essentially characterized by the following facts : a) Voters have identical first TCA factor score, where TCA designates taxicab correspondence analysis, an L1 variant of correspondence analysis ; b) Any preference is easily interpreted as riffle shuffling of its items ; c) The nature of different riffle shuffling of items can be seen in the structure of the contingency table of the first-order marginals constructed from the Borda scorings of the voters ; d) The first TCA factor scores of the items of a coherent cluster are interpreted as Borda scale of the items. We also introduce a crossing index, which measures the extent of crossing of scores of voters between the two blocks seriation of the items. The novel approach is explained on the benchmarking SUSHI data set, where we show that this data set has a very simple structure, which can also be communicated in a tabular form.
翻译:(d) 我们的主要任务是通过一个探索性拼接打乱程序发现和显示观察到的等级数据结构,该程序按顺序将n选民分解成数量有限的连贯小组,加上一个吵闹小组:在吵闹小组代表出局选民,每个一致小组由数量有限的一致分组组成;我们认为,对一组物品进行试打打打乱,相当于两个区块之间有一定分数的项目进行最佳的两个区块打乱。在其连贯的小组内,一个拼凑一致的选民组群基本上以下列事实为特征:a)选民拥有相同的TCA因数第一分,而TCA指定了税卡函分析,一个L1类对应分析变式;b)任何偏好都很容易被解释为其物品打乱;c)在应急表结构中可以看到不同调动的项目的性质,两个区块之间有些得分。从Borda的评分中得出第一级边缘边缘的选民群群群群群群群,我们还可以在其中解释一个等级等级等级等级等级等级等级的等级表。