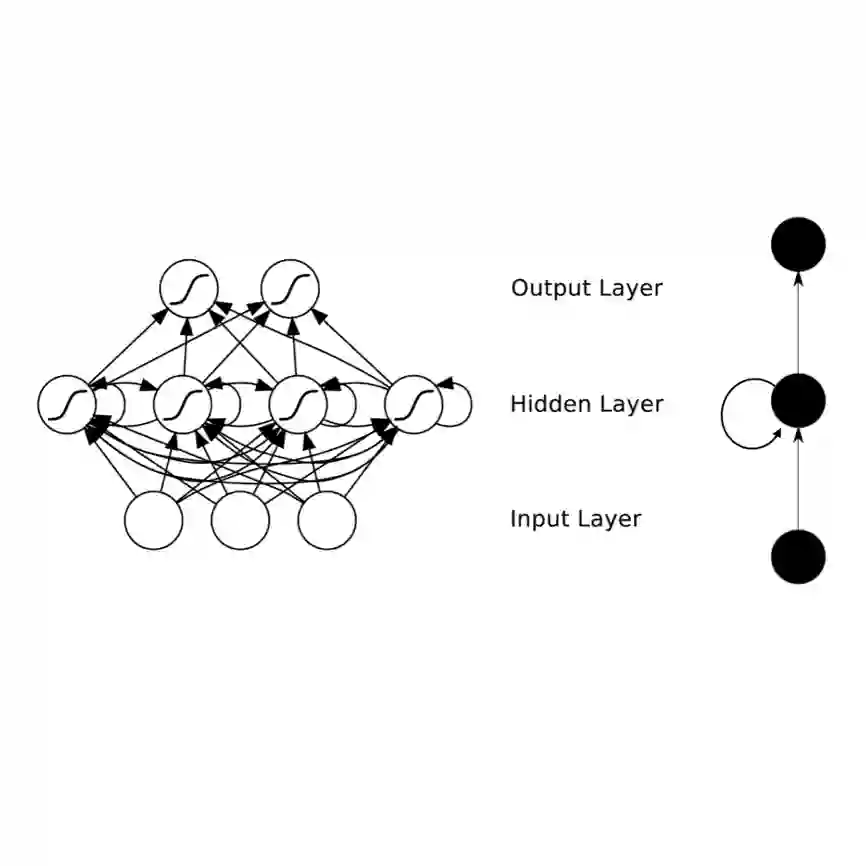
Recurrent neural networks are capable of learning the dynamics of an unknown nonlinear system purely from input-output measurements. However, the resulting models do not provide any stability guarantees on the input-output mapping. In this work, we represent a recurrent neural network as a linear time-invariant system with nonlinear disturbances. By introducing constraints on the parameters, we can guarantee finite gain stability and incremental finite gain stability. We apply this identification method to learn the motion of a four-degrees-of-freedom ship that is moving in open water and compare it against other purely learning-based approaches with unconstrained parameters. Our analysis shows that the constrained recurrent neural network has a lower prediction accuracy on the test set, but it achieves comparable results on an out-of-distribution set and respects stability conditions.
翻译:经常性神经网络能够完全从输入-输出测量中了解未知的非线性系统动态。 但是, 所产生的模型并不能为输入- 输出绘图提供任何稳定性保障。 在这项工作中, 我们代表一个经常性神经网络, 作为线性时间变化系统, 具有非线性扰动。 通过对参数施加限制, 我们可以保证有限收益的稳定性和递增有限收益的稳定性。 我们使用这种识别方法来学习在开阔水域移动的四度自由船的动向, 并与其他纯粹以学习为基础的方法和非限制参数进行比较。 我们的分析表明, 受限制的经常性神经网络在测试集上预测准确性较低, 但是在分布图上可以取得类似的结果, 并且尊重稳定性条件 。