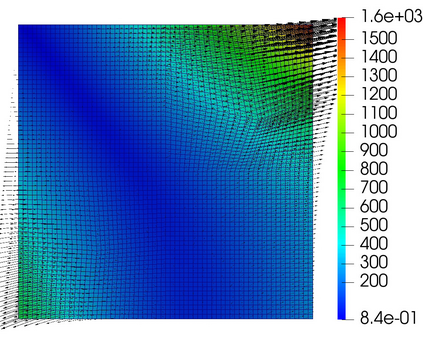
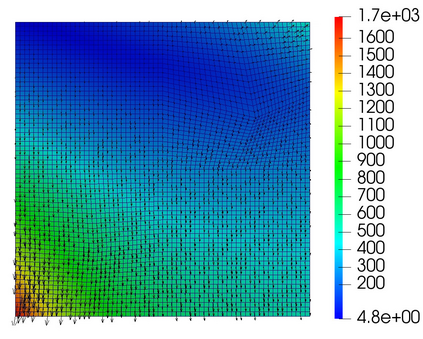
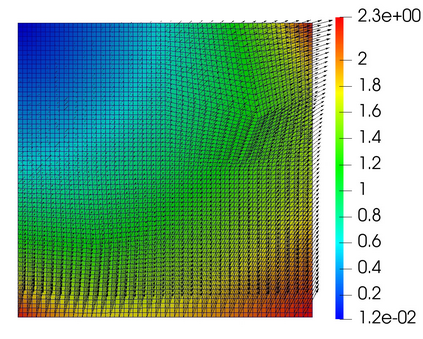
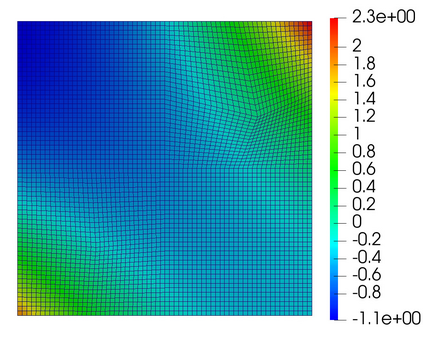
We develop non-overlapping domain decomposition methods for the Biot system of poroelasticity in a mixed form. The solid deformation is modeled with a mixed three-field formulation with weak stress symmetry. The fluid flow is modeled with a mixed Darcy formulation. We introduce displacement and pressure Lagrange multipliers on the subdomain interfaces to impose weakly continuity of normal stress and normal velocity, respectively. The global problem is reduced to an interface problem for the Lagrange multipliers, which is solved by a Krylov space iterative method. We study both monolithic and split methods. In the monolithic method, a coupled displacement-pressure interface problem is solved, with each iteration requiring the solution of local Biot problems. We show that the resulting interface operator is positive definite and analyze the convergence of the iteration. We further study drained split and fixed stress Biot splittings, in which case we solve separate interface problems requiring elasticity and Darcy solves. We analyze the stability of the split formulations. Numerical experiments are presented to illustrate the convergence of the domain decomposition methods and compare their accuracy and efficiency.
翻译:我们以混合形式开发了不重叠的广度生物系域分解方法。 固态变形的模型是三维混合配方, 压力对称性弱。 流体流的模型是混合的达西配方。 我们在子域界面上引入置换和压力拉格朗变异器, 分别将正常应力和正常速度的连续性降低到微弱。 全球问题被降为拉格朗变异器的界面问题, 由克里洛夫空间迭接合法解决。 我们研究了单体和分裂方法。 在单体方法中, 混合置换- 压力界面问题得到解决, 每次循环都要求解决本地生物问题。 我们显示, 由此产生的接口操作者是肯定的, 分析迭代作用的趋同。 我们进一步研究分解和固定的应力 Biot 分解, 从而解决需要弹性和达西解的单独接口问题。 我们分析了分裂配方的稳定性。 我们用数字实验展示了分解法的趋同性, 并分析其精确性。