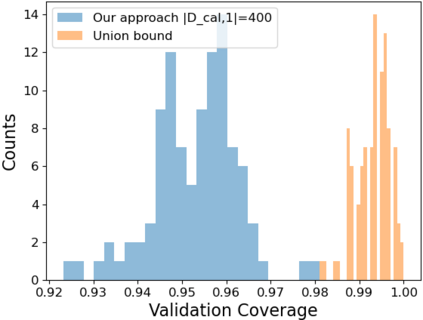
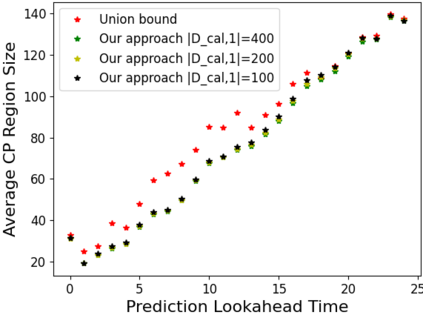
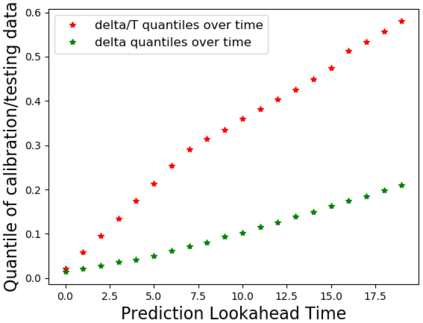
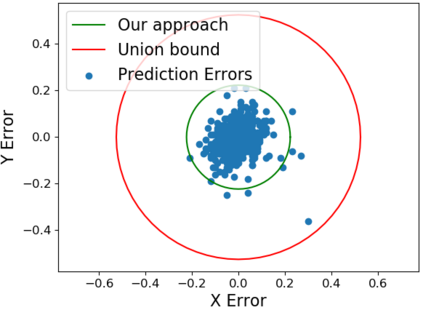
Conformal prediction is a statistical tool for producing prediction regions of machine learning models that are valid with high probability. However, applying conformal prediction to time series data leads to conservative prediction regions. In fact, to obtain prediction regions over $T$ time steps with confidence $1-\delta$, {previous works require that each individual prediction region is valid} with confidence $1-\delta/T$. We propose an optimization-based method for reducing this conservatism to enable long horizon planning and verification when using learning-enabled time series predictors. Instead of considering prediction errors individually at each time step, we consider a parameterized prediction error over multiple time steps. By optimizing the parameters over an additional dataset, we find prediction regions that are not conservative. We show that this problem can be cast as a mixed integer linear complementarity program (MILCP), which we then relax into a linear complementarity program (LCP). Additionally, we prove that the relaxed LP has the same optimal cost as the original MILCP. Finally, we demonstrate the efficacy of our method on case studies using pedestrian trajectory predictors and F16 fighter jet altitude predictors.
翻译:暂无翻译