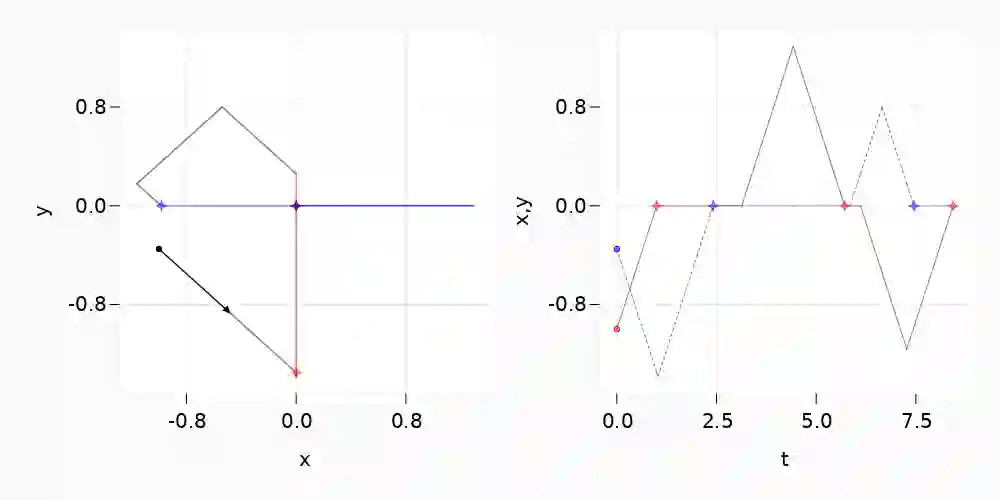
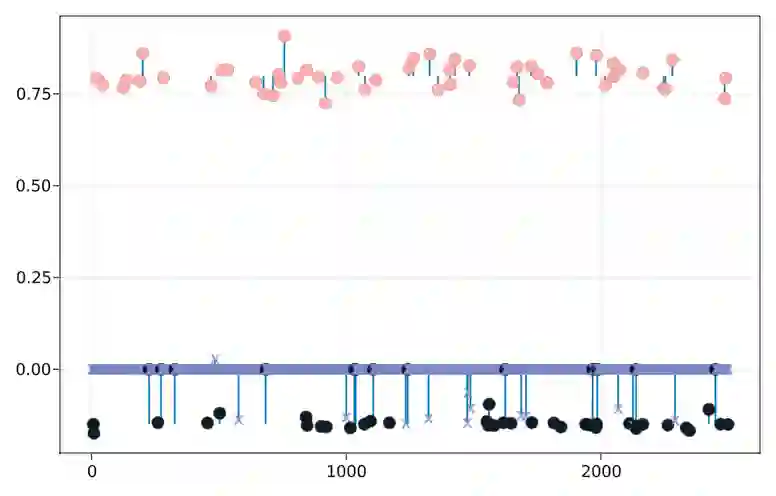
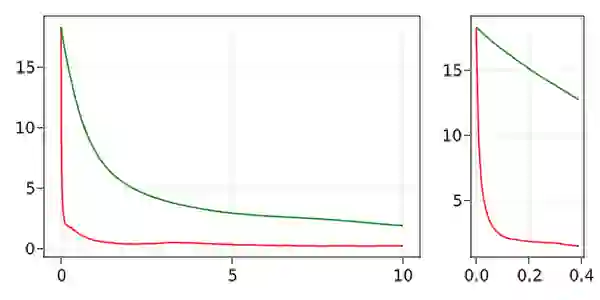
We construct a new class of efficient Monte Carlo methods based on continuous-time piecewise deterministic Markov processes (PDMPs) suitable for inference in high dimensional sparse models, i.e. models for which there is prior knowledge that many coordinates are likely to be exactly $0$. This is achieved with the fairly simple idea of endowing existing PDMP samplers with 'sticky' coordinate axes, coordinate planes etc. Upon hitting those subspaces, an event is triggered during which the process sticks to the subspace, this way spending some time in a sub-model. This results in non-reversible jumps between different (sub-)models. While we show that PDMP samplers in general can be made sticky, we mainly focus on the Zig-Zag sampler. The computational efficiency of our method (and implementation) is established through numerical experiments where both the sample size and the dimension of the parameter space are large.
翻译:我们根据连续的片段确定性马可夫工艺(PDMPs),根据适合高维分散模型(即以前知道许多坐标可能完全为0美元的模型)推断的连续片段确定性马可夫工艺(PDMPs),构建了新型高效的蒙特卡洛方法。这是通过将现有的PDMP采样器用“粘性”坐标轴、坐标平面等赋予相当简单的想法来实现的。在击中这些子空间时,会触发一个过程粘贴到子空间的事件,在子模型中花费一些时间。这导致不同(子)模型之间发生不可逆的跳跃。这导致不同(子)模型之间的不可逆跳跃。虽然我们显示PDMP采样器一般可以粘贴,但我们主要侧重于Zig-Zag采样器。我们方法(和实施)的计算效率是通过数字实验确定的,这里的样本大小和参数空间的尺寸都很大。