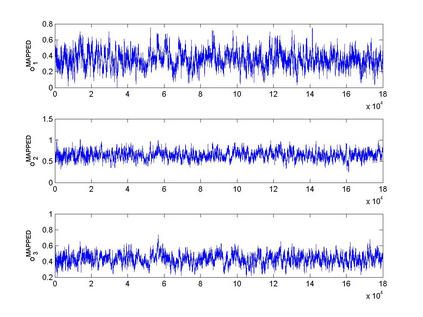
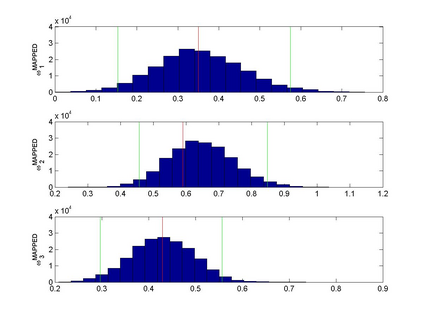
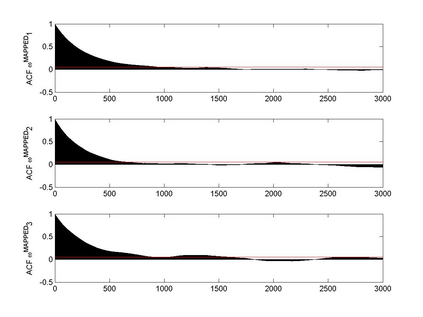
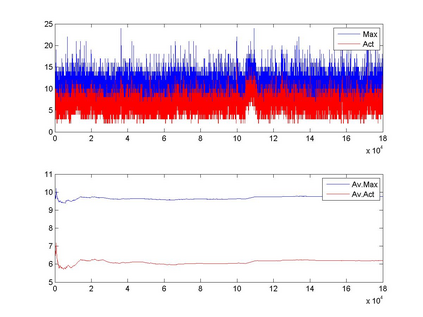
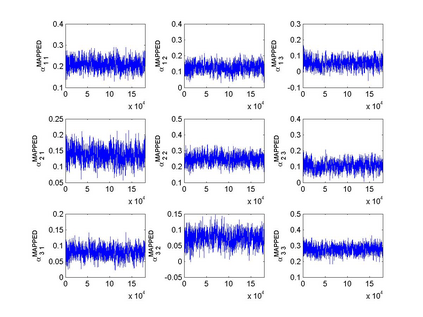
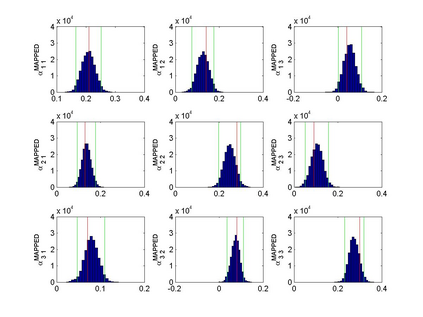
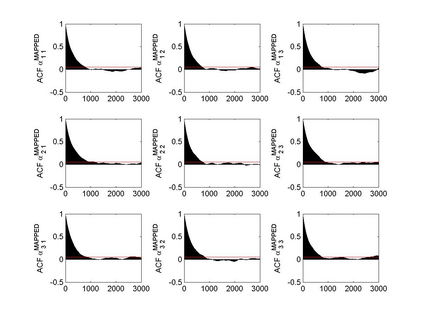
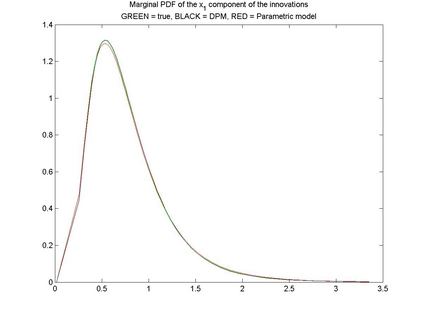
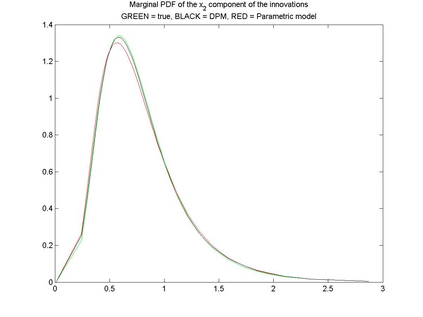
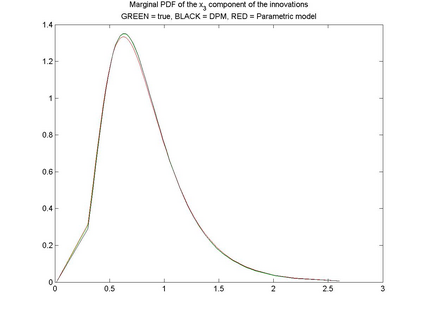
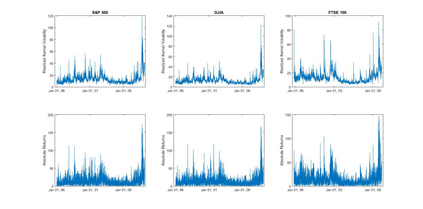
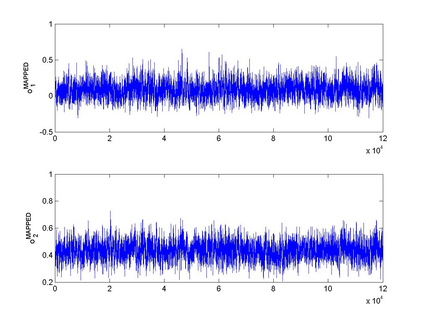
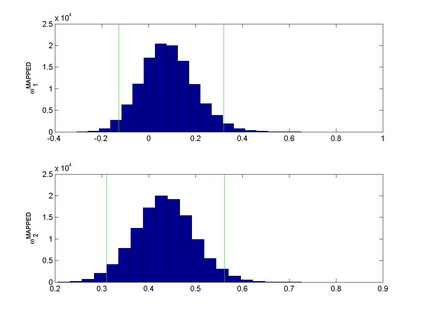
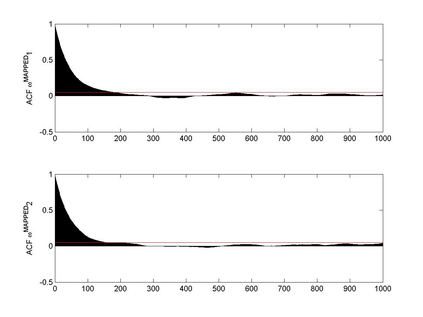
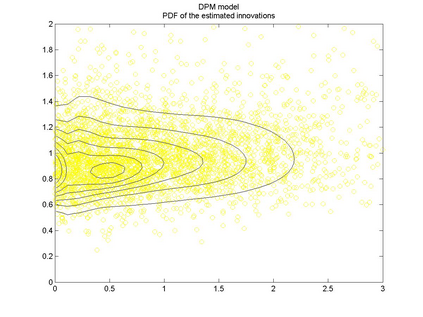
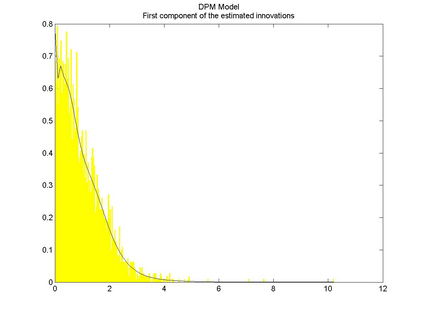
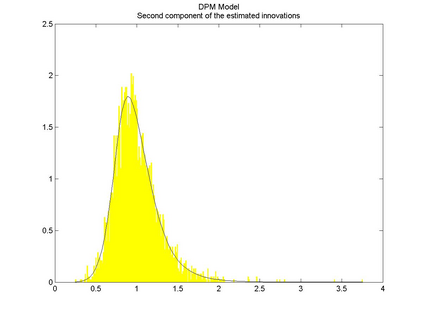
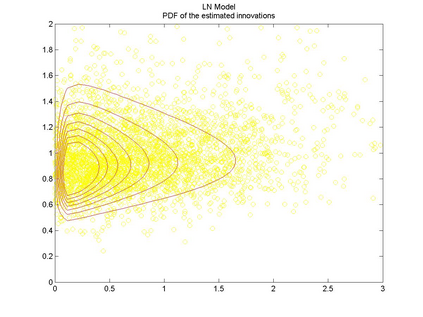
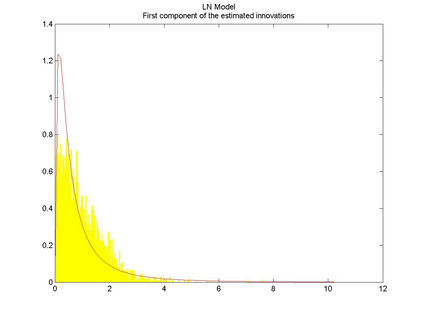
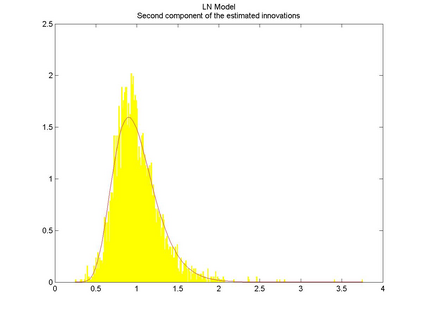
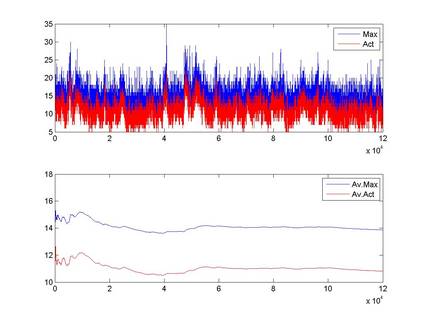
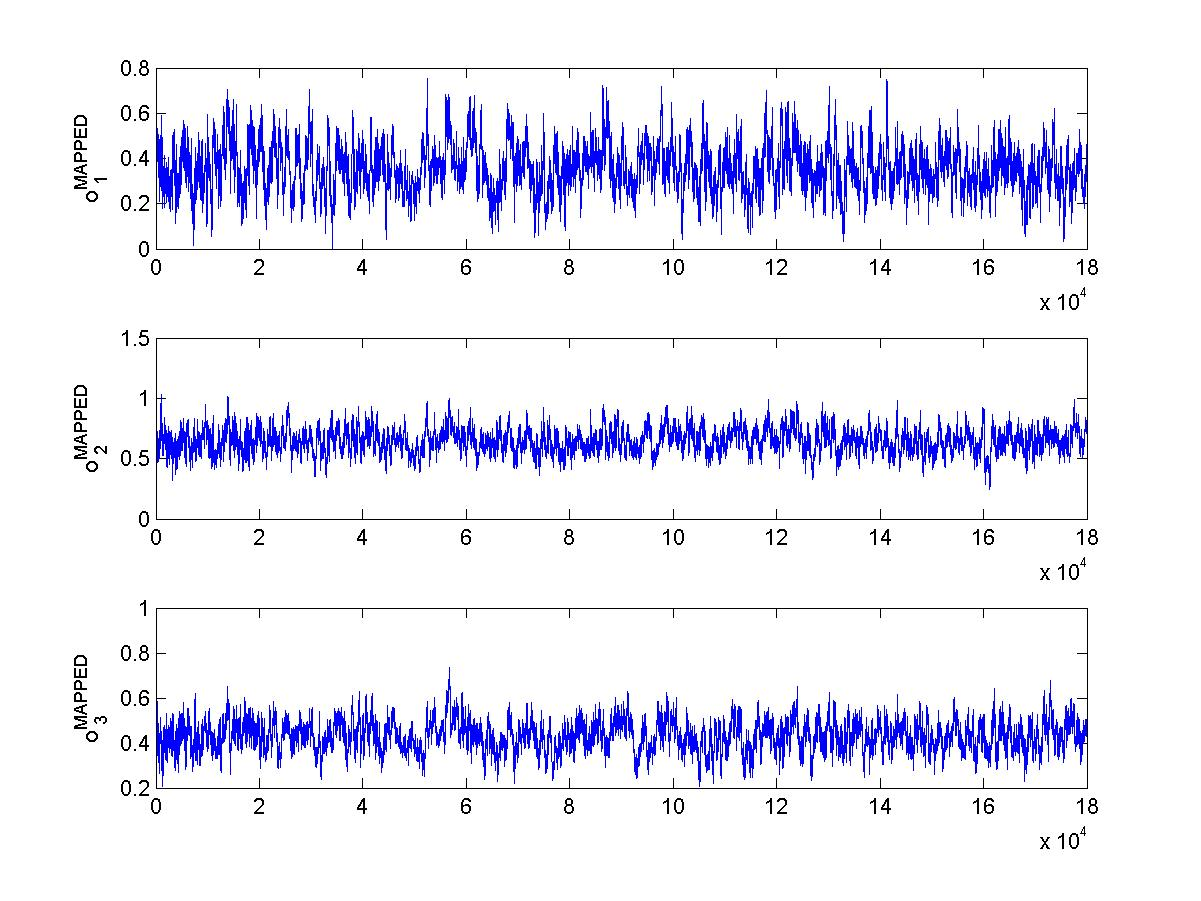
Interactions among multiple time series of positive random variables are crucial in diverse financial applications, from spillover effects to volatility interdependence. A popular model in this setting is the vector Multiplicative Error Model (vMEM) which poses a linear iterative structure on the dynamics of the conditional mean, perturbed by a multiplicative innovation term. A main limitation of vMEM is however its restrictive assumption on the distribution of the random innovation term. A Bayesian semiparametric approach that models the innovation vector as an infinite location-scale mixture of multidimensional kernels with support on the positive orthant is used to address this major shortcoming of vMEM. Computational complications arising from the constraints to the positive orthant are avoided through the formulation of a slice sampler on the parameter-extended unconstrained version of the model. The method is applied to simulated and real data and a flexible specification is obtained that outperforms the classical ones in terms of fitting and predictive power.
翻译:从溢出效应到波动性相互依存等多种金融应用中,积极随机变量的多重时间序列相互作用至关重要。在这一背景下,一个流行的模式是矢量倍增错误模型(vMEM),该模型对受多复制性创新术语干扰的有条件平均值动态构成线性迭代结构。VMEM的主要局限性在于它对随机创新术语分布的限制性假设。一种巴伊西亚半参数方法,将创新矢量作为无限的多层次多层内核混合物,在支持正态或强度的情况下,用来应对 vMEM的这一重大缺陷。通过在参数扩展的模型未受限制的版本上配制切片取样器,避免了因正态或强的制约而产生的计算并发症。该方法用于模拟和真实数据,并获得一种灵活的规格,在适应和预测能力方面超越了经典的典型。