Measure Theoretic Reeb Graphs and Reeb Spaces

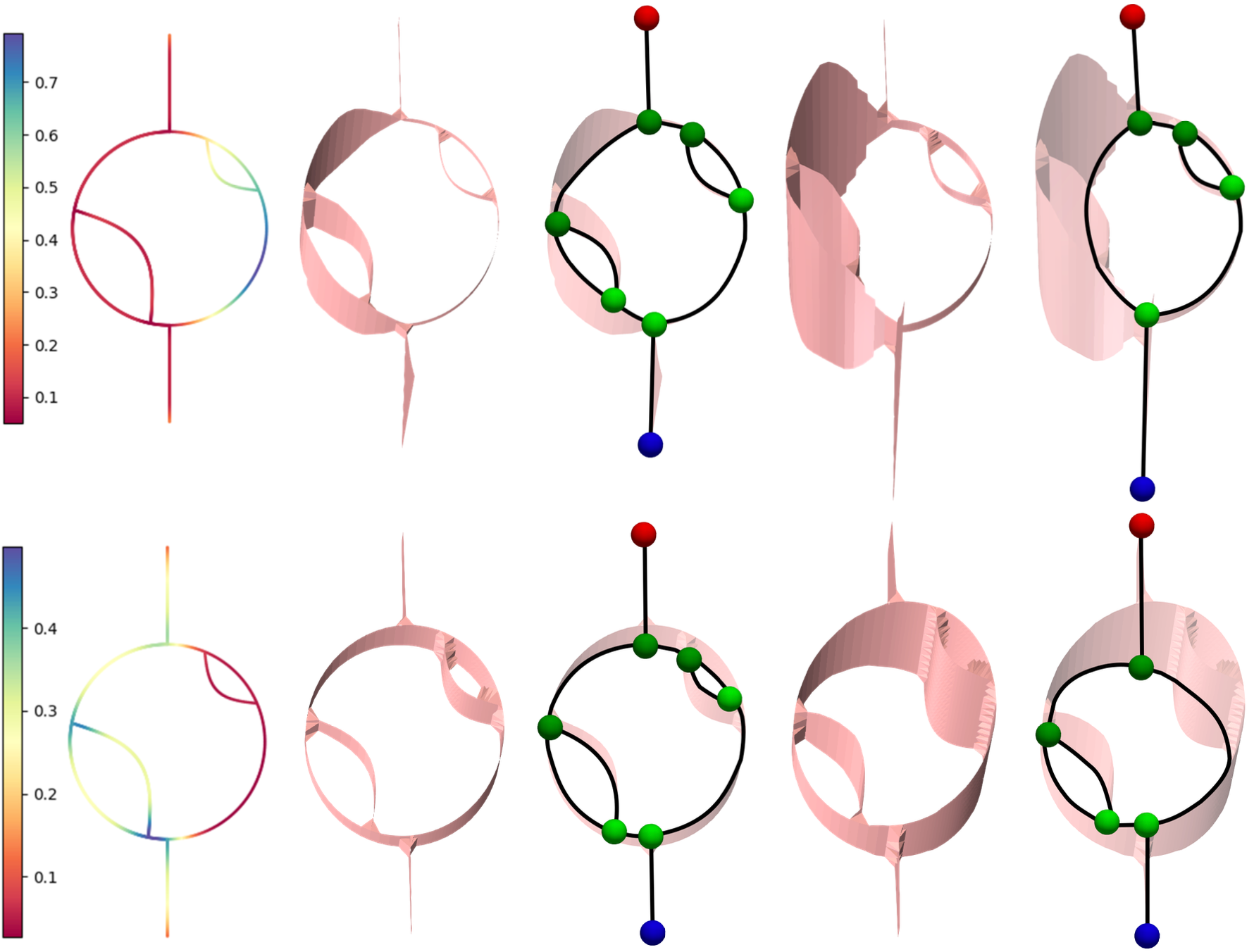
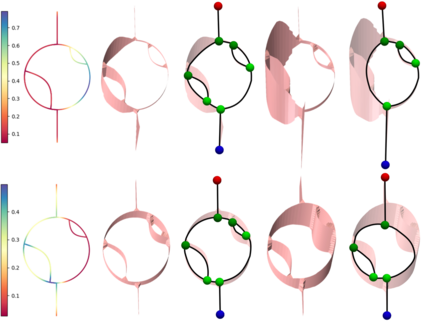
A Reeb graph is a graphical representation of a scalar function $f: X \to \mathbb{R}$ on a topological space $X$ that encodes the topology of the level sets. A Reeb space is a generalization of the Reeb graph to a multivariate function $f: X \to \mathbb{R}^d$. In this paper, we propose novel constructions of Reeb graphs and Reeb spaces that incorporate the use of a measure. Specifically, we introduce measure theoretic Reeb graphs and Reeb spaces when the domain or the range is modeled as a metric measure space (i.e.,~a metric space equipped with a measure). Our main goal is to enhance the robustness of the Reeb graph and Reeb space in representing the topological features of a scalar field while accounting for the distribution of the measure. We first prove the stability of our measure theoretic constructions with respect to the interleaving distance. We then prove their stability with respect to the measure, defined using the distance to a measure or the kernel distance to a measure, respectively.