Preconditioners for robust optimal control problems under uncertainty

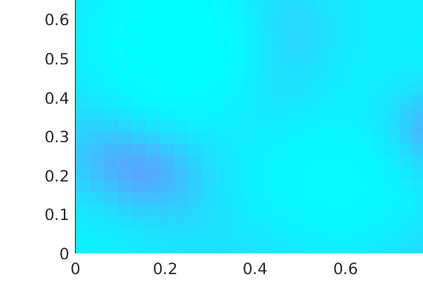
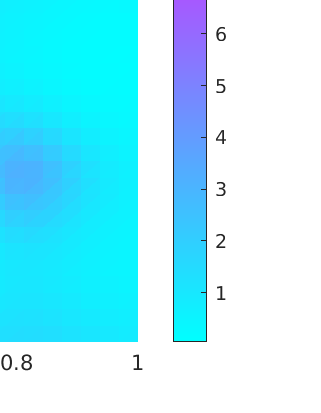
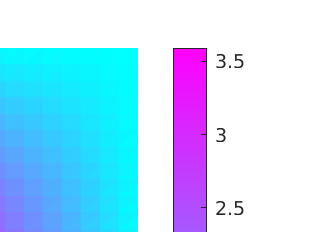
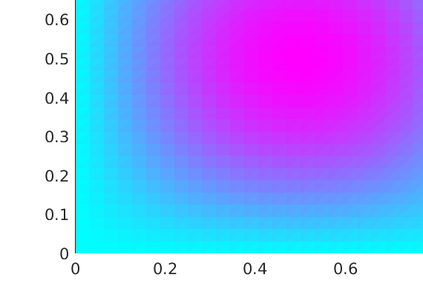
The discretization of robust quadratic optimal control problems under uncertainty using the finite element method and the stochastic collocation method leads to large saddle-point systems, which are fully coupled across the random realizations. Despite its relevance for numerous engineering problems, the solution of such systems is notoriusly challenging. In this manuscript, we study efficient preconditioners for all-at-once approaches using both an algebraic and an operator preconditioning framework. We show in particular that for values of the regularization parameter not too small, the saddle-point system can be efficiently solved by preconditioning in parallel all the state and adjoint equations. For small values of the regularization parameter, robustness can be recovered by the additional solution of a small linear system, which however couples all realizations. A mean approximation and a Chebyshev semi-iterative method are investigated to solve this reduced system. Our analysis considers a random elliptic partial differential equation whose diffusion coefficient $\kappa(x,\omega)$ is modeled as an almost surely continuous and positive random field, though not necessarily uniformly bounded and coercive. We further provide estimates on the dependence of the preconditioned system on the variance of the random field. Such estimates involve either the first or second moment of the random variables $1/\min_{x\in \overline{D}} \kappa(x,\omega)$ and $\max_{x\in \overline{D}}\kappa(x,\omega)$, where $D$ is the spatial domain. The theoretical results are confirmed by numerical experiments, and implementation details are further addressed.