RANG: A Residual-based Adaptive Node Generation Method for Physics-Informed Neural Networks

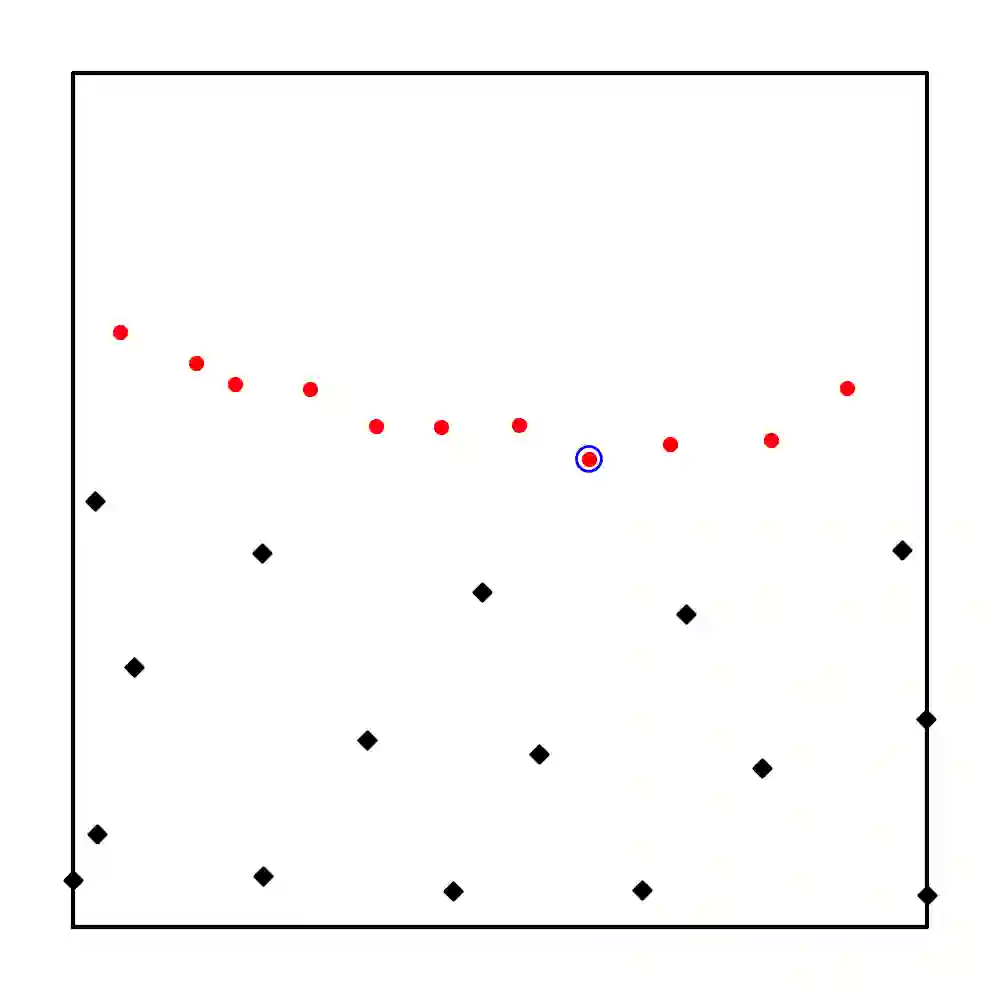
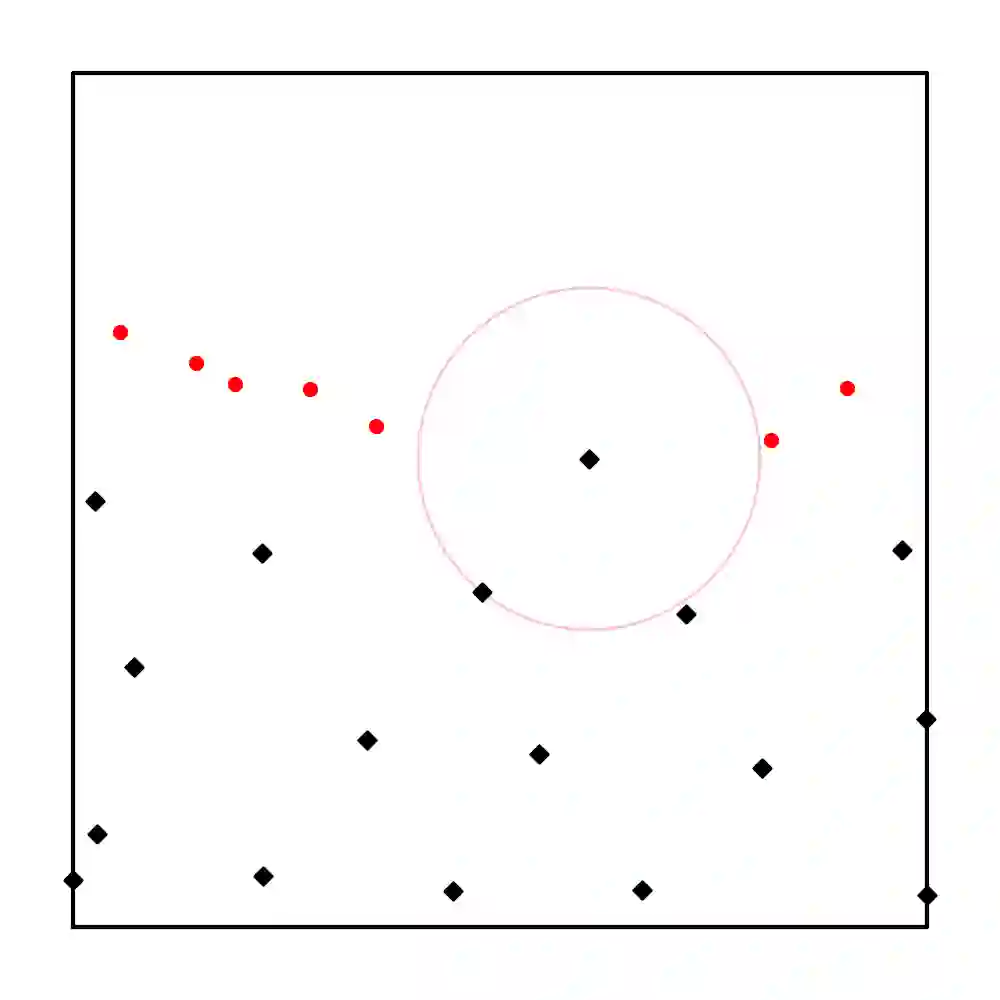
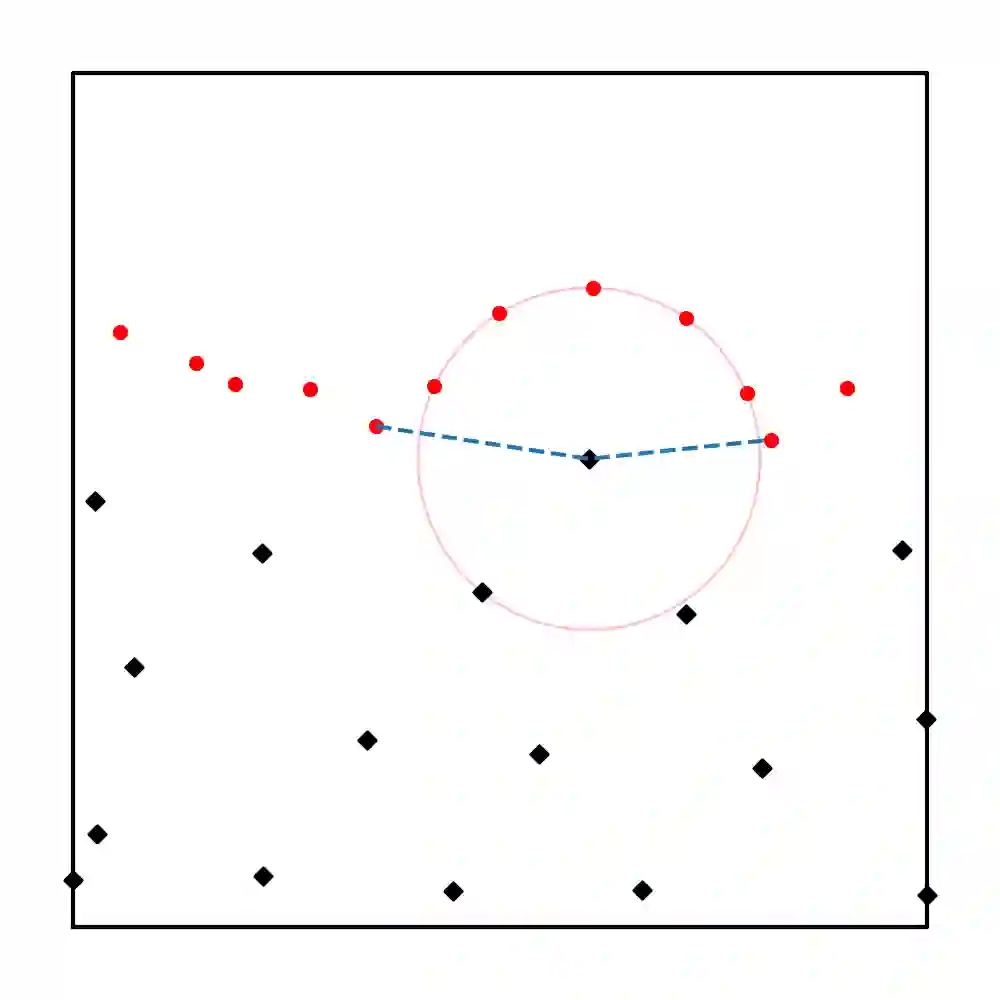
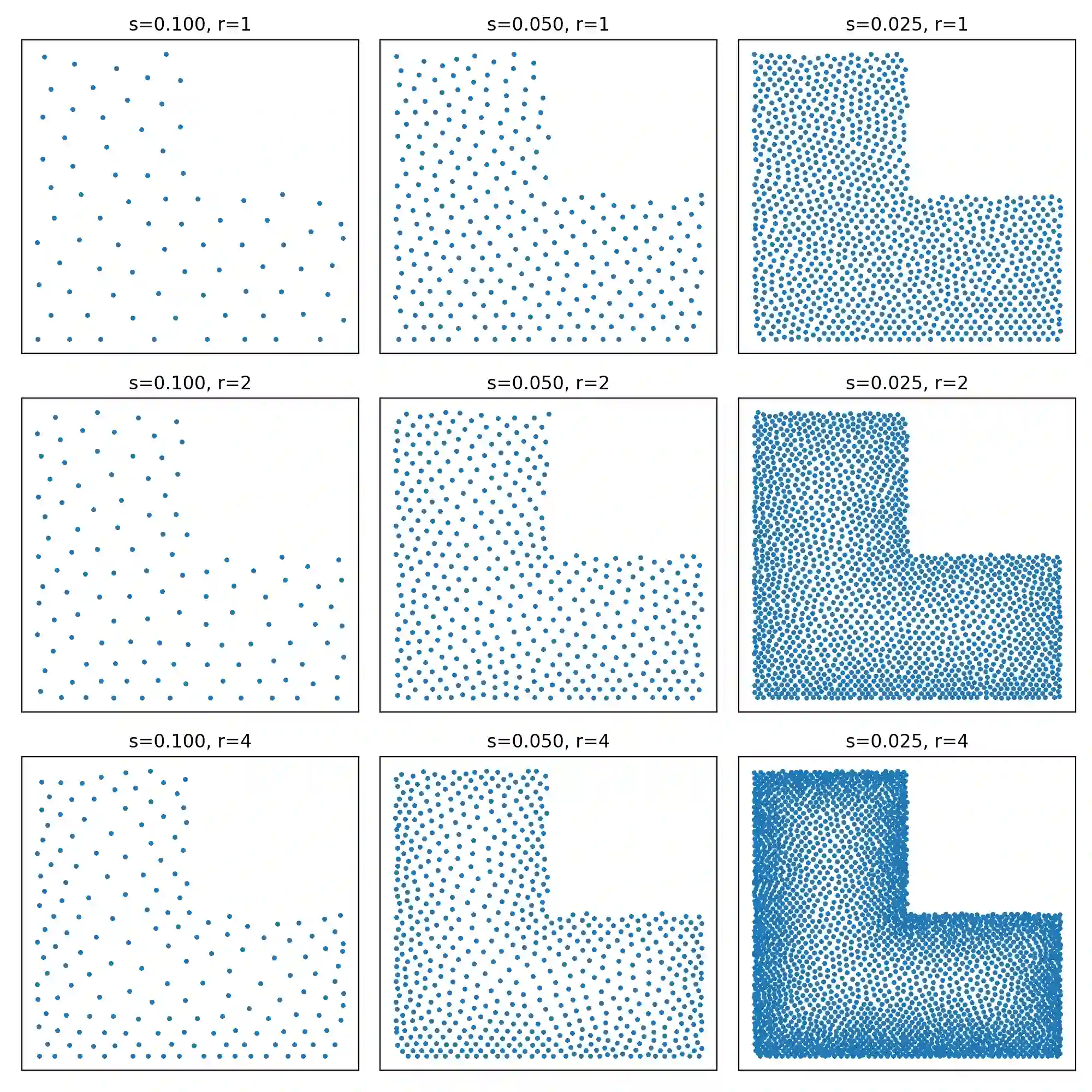
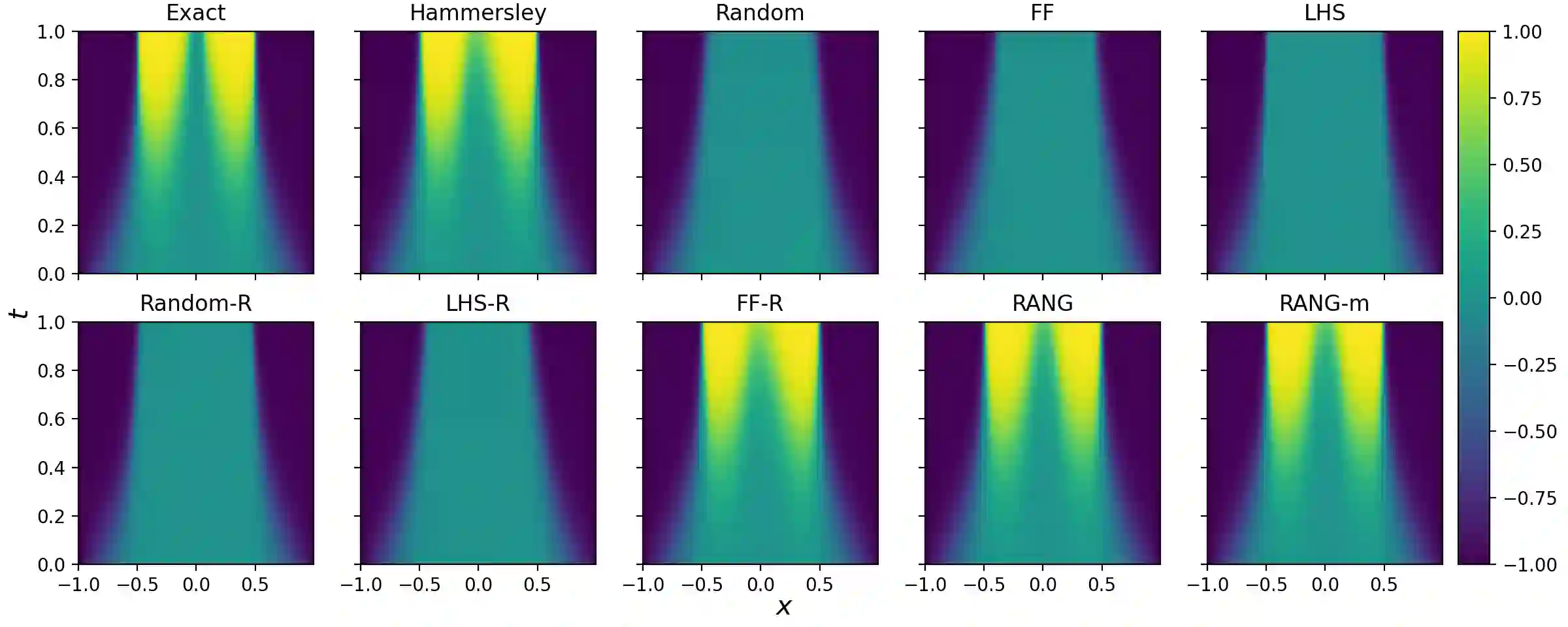
Learning solutions of partial differential equations (PDEs) with Physics-Informed Neural Networks(PINNs) is an attractive alternative approach to traditional solvers due to its flexibility and ease of incorporating observed data. Despite the success of PINNs in accurately solving a wide variety of PDEs, the method still requires improvements in terms of computational efficiency. One possible improvement idea is to optimize the generation of training point sets. Residual-based adaptive sampling and quasi-uniform sampling approaches have been each applied to improve the training effects of PINNs, respectively. To benefit from both methods, we propose the Residual-based Adaptive Node Generation (RANG) approach for efficient training of PINNs, which is based on a variable density nodal distribution method for RBF-FD. The method is also enhanced by a memory mechanism to further improve training stability. We conduct experiments on three linear PDEs and three nonlinear PDEs with various node generation methods, through which the accuracy and efficiency of the proposed method compared to the predominant uniform sampling approach is verified numerically.