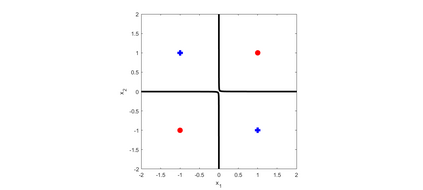
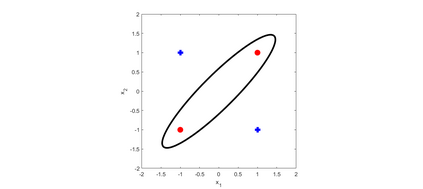
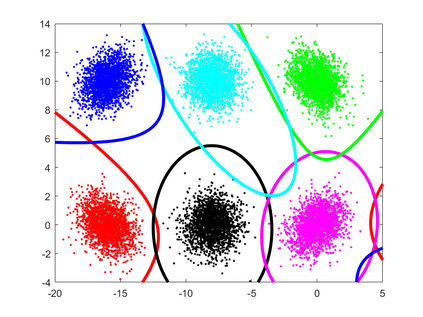
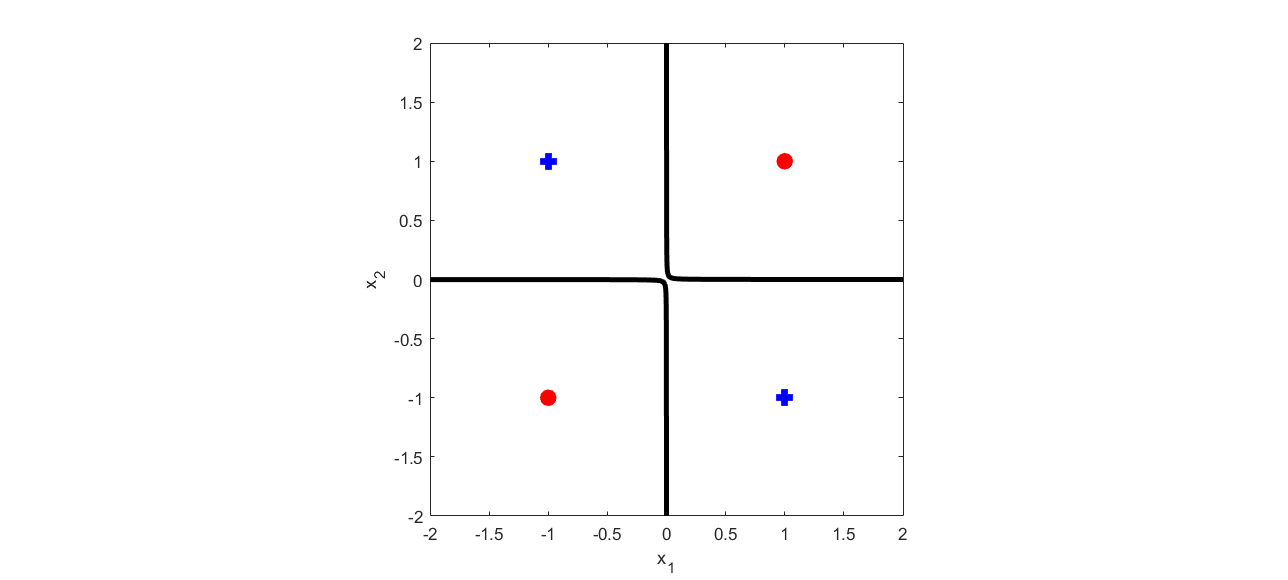
Higher order artificial neurons whose outputs are computed by applying an activation function to a higher order multinomial function of the inputs have been considered in the past, but did not gain acceptance due to the extra parameters and computational cost. However, higher order neurons have significantly greater learning capabilities since the decision boundaries of higher order neurons can be complex surfaces instead of just hyperplanes. The boundary of a single quadratic neuron can be a general hyper-quadric surface allowing it to learn many nonlinearly separable datasets. Since quadratic forms can be represented by symmetric matrices, only $\frac{n(n+1)}{2}$ additional parameters are needed instead of $n^2$. A quadratic Logistic regression model is first presented. Solutions to the XOR problem with a single quadratic neuron are considered. The complete vectorized equations for both forward and backward propagation in feedforward networks composed of quadratic neurons are derived. A reduced parameter quadratic neural network model with just $ n $ additional parameters per neuron that provides a compromise between learning ability and computational cost is presented. Comparison on benchmark classification datasets are used to demonstrate that a final layer of quadratic neurons enables networks to achieve higher accuracy with significantly fewer hidden layer neurons. In particular this paper shows that any dataset composed of $C$ bounded clusters can be separated with only a single layer of $C$ quadratic neurons.
翻译:暂无翻译