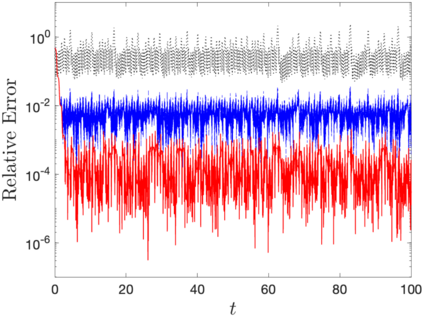
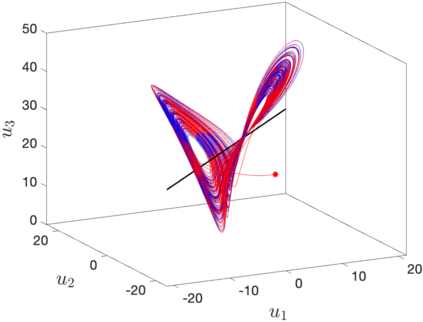
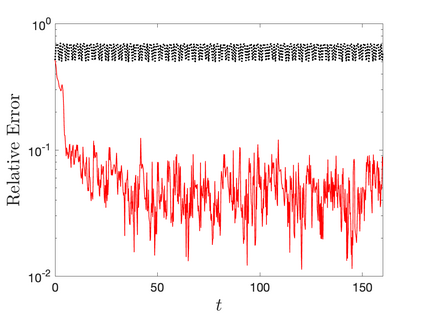
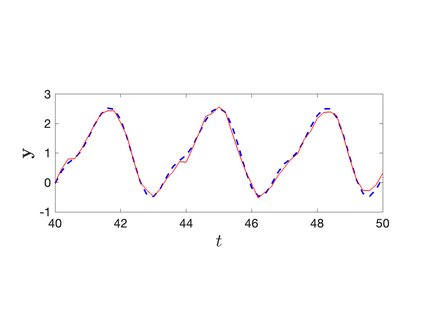
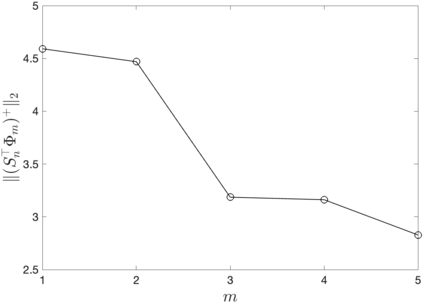
Discrete empirical interpolation method (DEIM) estimates a function from its incomplete pointwise measurements. Unfortunately, DEIM suffers large interpolation errors when few measurements are available. Here, we introduce Sparse DEIM (S-DEIM) for accurately estimating a function even when very few measurements are available. To this end, S-DEIM leverages a kernel vector which has been neglected in previous DEIM-based methods. We derive theoretical error estimates for S-DEIM, showing its relatively small error when an optimal kernel vector is used. When the function is generated by a continuous-time dynamical system, we propose a data assimilation algorithm which approximates the optimal kernel vector using observational time series. We prove that, under certain conditions, data assimilated S-DEIM converges exponentially fast towards the true state. We demonstrate the efficacy of our method on two numerical examples.
翻译:暂无翻译