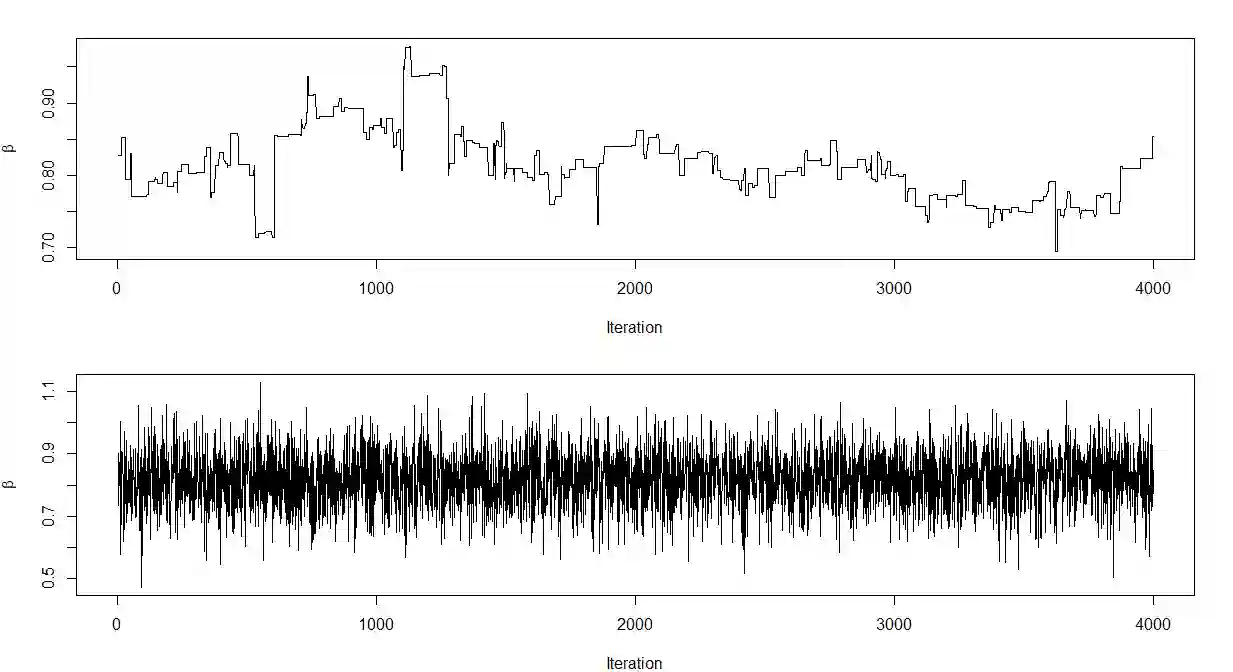
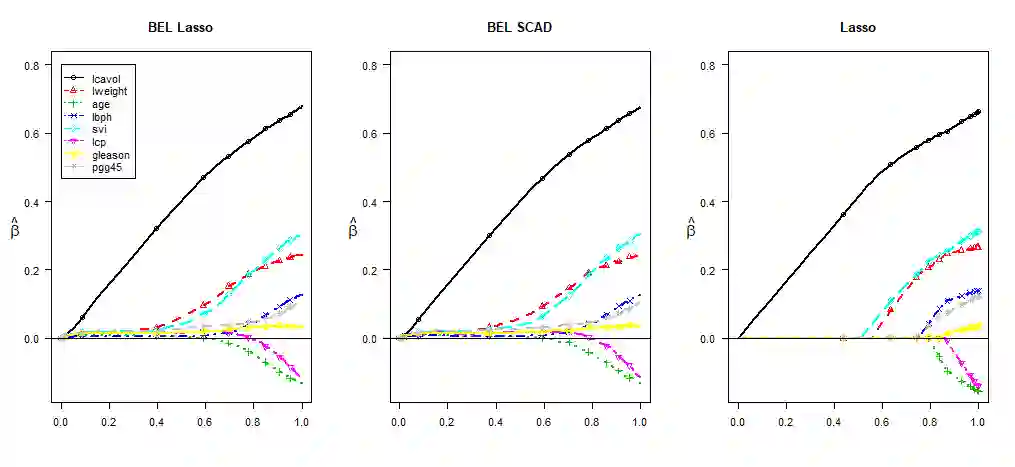
Empirical likelihood is a popular nonparametric statistical tool that does not require any distributional assumptions. In this paper, we explore the possibility of conducting variable selection via Bayesian empirical likelihood. We show theoretically that when the prior distribution satisfies certain mild conditions, the corresponding Bayesian empirical likelihood estimators are posteriorly consistent and variable selection consistent. As special cases, we show the prior of Bayesian empirical likelihood LASSO and SCAD satisfies such conditions and thus can identify the non-zero elements of the parameters with probability tending to 1. In addition, it is easy to verify that those conditions are met for other widely used priors such as ridge, elastic net and adaptive LASSO. Empirical likelihood depends on a parameter that needs to be obtained by numerically solving a non-linear equation. Thus, there exists no conjugate prior for the posterior distribution, which causes the slow convergence of the MCMC sampling algorithm in some cases. To solve this problem, we propose a novel approach, which uses an approximation distribution as the proposal. The computational results demonstrate quick convergence for the examples used in the paper. We use both simulation and real data analyses to illustrate the advantages of the proposed methods.
翻译:在本文中,我们探索了通过巴伊西亚实证可能性进行可变选择的可能性。我们从理论上表明,当先前的分布满足某些温和条件时,相应的巴伊西亚实证可能性估计数是相继一致和可变选择一致的。作为特例,我们展示了巴伊西亚实证可能性LASSO和SCAD先前满足了这些条件,从而可以确定参数中的非零要素,概率为1。此外,我们提出一种新颖的办法,用近似分布法作为建议。计算结果表明,本文使用的例子迅速趋同。我们使用模拟法和真实数据分析法来说明拟议数据分析的优点。我们使用模拟法和真实数据分析法来说明拟议数据分析的优点。