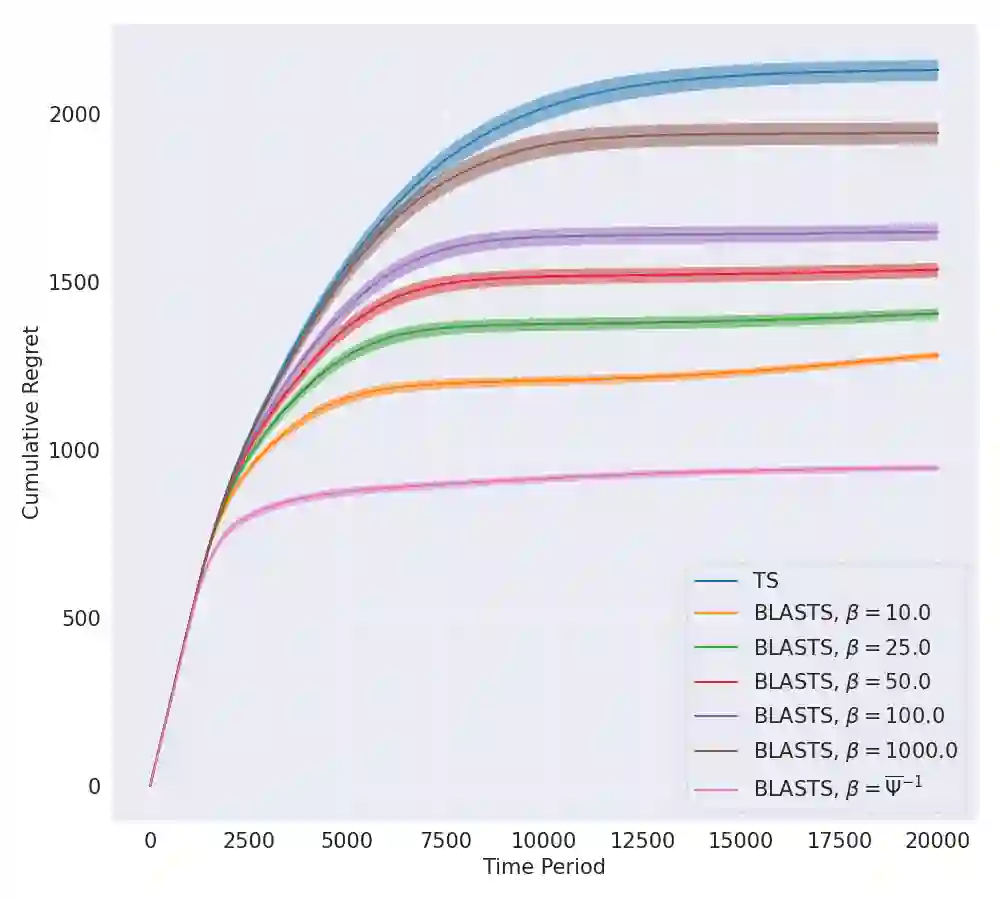
Agents that learn to select optimal actions represent a prominent focus of the sequential decision-making literature. In the face of a complex environment or constraints on time and resources, however, aiming to synthesize such an optimal policy can become infeasible. These scenarios give rise to an important trade-off between the information an agent must acquire to learn and the sub-optimality of the resulting policy. While an agent designer has a preference for how this trade-off is resolved, existing approaches further require that the designer translate these preferences into a fixed learning target for the agent. In this work, leveraging rate-distortion theory, we automate this process such that the designer need only express their preferences via a single hyperparameter and the agent is endowed with the ability to compute its own learning targets that best achieve the desired trade-off. We establish a general bound on expected discounted regret for an agent that decides what to learn in this manner along with computational experiments that illustrate the expressiveness of designer preferences and even show improvements over Thompson sampling in identifying an optimal policy.
翻译:学会选择最佳行动的代理商代表了顺序决策文献的突出焦点。然而,面对复杂的环境或时间和资源的制约,旨在综合这种最佳政策的目标可能变得不可行。这些假设在代理商必须获得的信息和由此产生的政策的次优性之间产生了重要的权衡。虽然代理商设计师偏好如何解决这一权衡,但现有办法进一步要求设计师将这些偏好转化为代理人的固定学习目标。在这项工作中,我们利用率扭曲理论,使这一过程自动化,使设计师只需通过单倍超准度来表达其偏好,而代理商具有能力来计算自己的学习目标,从而最能实现理想的权衡。我们规定,对于决定以这种方式学习内容的代理商,在进行计算实验以说明设计师偏好的明确性,甚至表明在确定最佳政策方面比汤普森抽样有所改进。