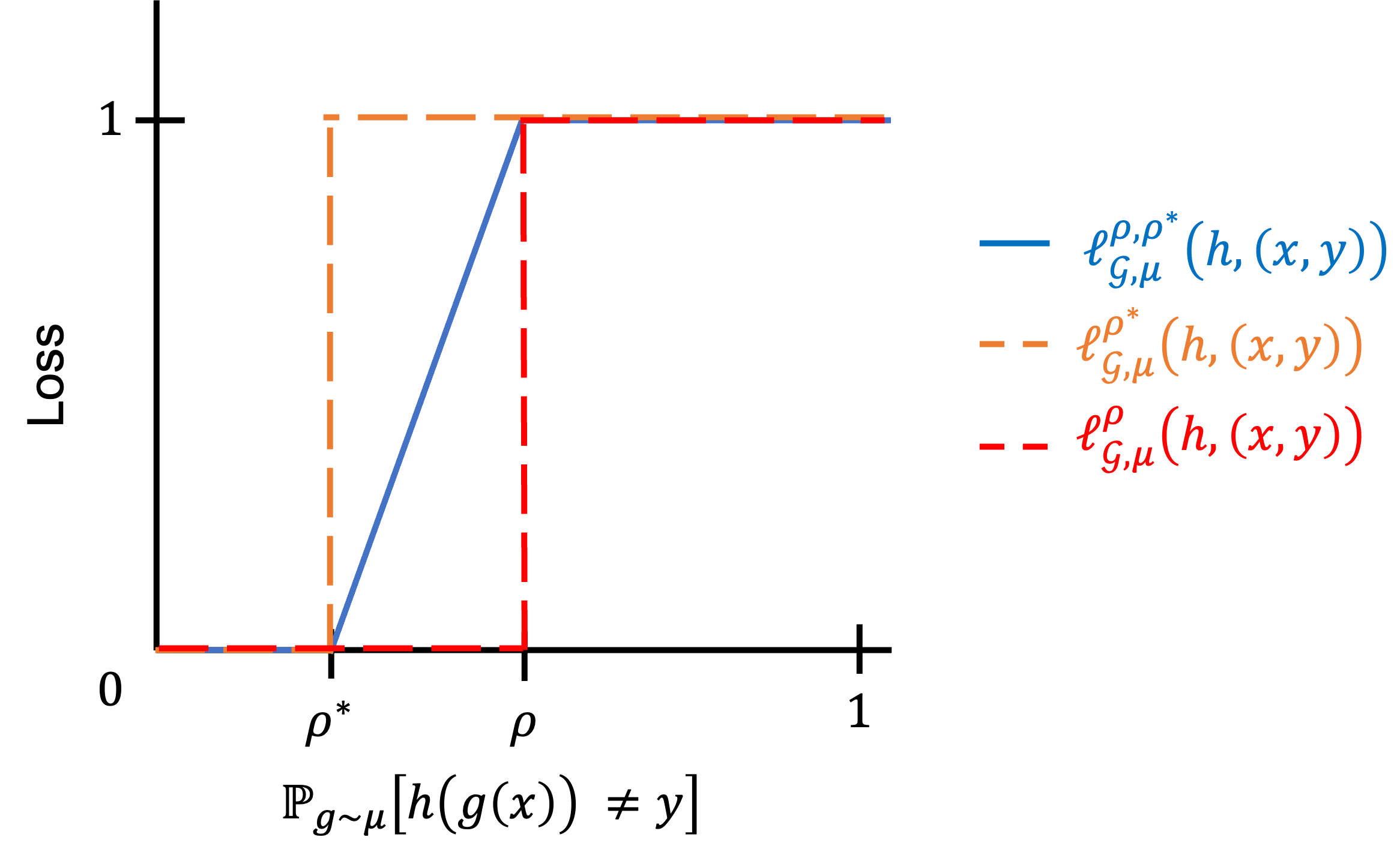
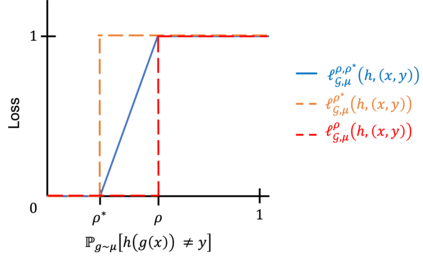
Recently, Robey et al. propose a notion of probabilistic robustness, which, at a high-level, requires a classifier to be robust to most but not all perturbations. They show that for certain hypothesis classes where proper learning under worst-case robustness is \textit{not} possible, proper learning under probabilistic robustness \textit{is} possible with sample complexity exponentially smaller than in the worst-case robustness setting. This motivates the question of whether proper learning under probabilistic robustness is always possible. In this paper, we show that this is \textit{not} the case. We exhibit examples of hypothesis classes $\mathcal{H}$ with finite VC dimension that are \textit{not} probabilistically robustly PAC learnable with \textit{any} proper learning rule. However, if we compare the output of the learner to the best hypothesis for a slightly \textit{stronger} level of probabilistic robustness, we show that not only is proper learning \textit{always} possible, but it is possible via empirical risk minimization.
翻译:最近, Robey 等人 提出了一个概率稳健性概念, 在高层次上, 要求分类者对大多数但并非所有扰动都保持稳健。 它们表明, 对于某些假设类, 在最坏情况稳健性下适当学习是可能的, 在一个概率稳健性 可能情况下, 样本复杂性指数比最坏情况稳健性环境大得多 的情况下, 适当学习。 这引发了一个问题: 在概率稳健性下适当学习是否总是可能的。 在本文中, 我们显示这是 \ textit{ not} 案例。 我们展示了一些假设类 $\ mathcal{H} 的例子, 具有有限的 VC 维度, 是\ textit{ no} 概率非常稳健的 PAC 可以学习 。 但是, 如果我们将学习者的输出量与 略微的 文本稳健性水平 最佳假设相比较, 我们显示, 我们不仅正确学习\ trextit { ways 的可能性, 但它是可能的实验性。