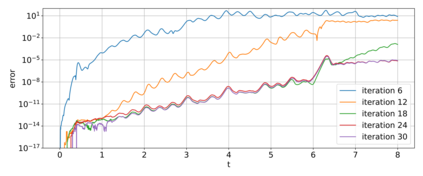
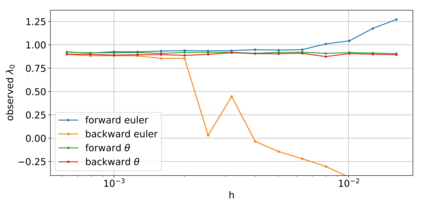
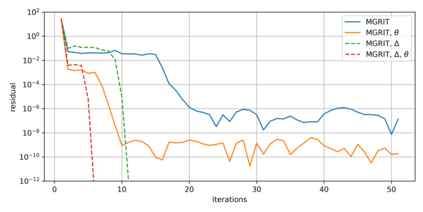
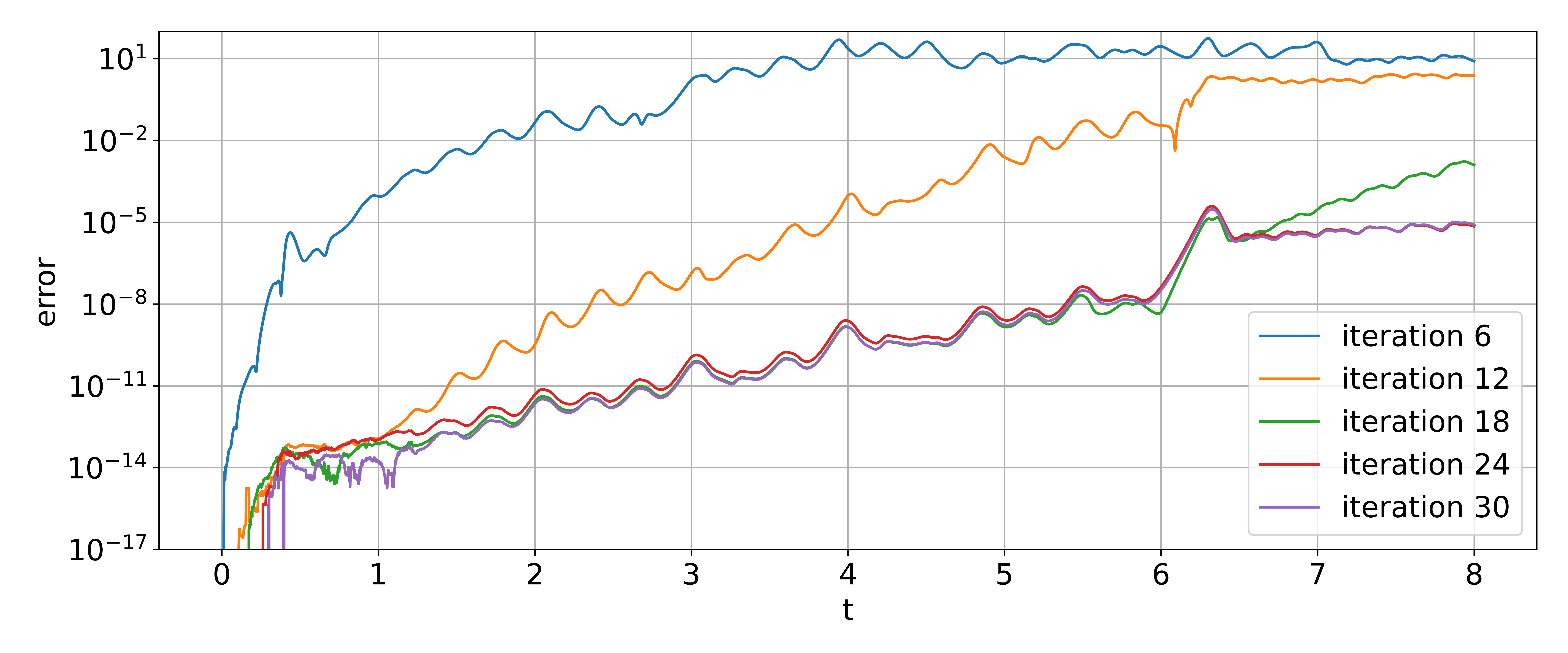
As CPU clock speeds have stagnated, and high performance computers continue to have ever higher core counts, increased parallelism is needed to take advantage of these new architectures. Traditional serial time-marching schemes are a significant bottleneck, as many types of simulations require large numbers of time-steps which must be computed sequentially. Parallel in Time schemes, such as the Multigrid Reduction in Time (MGRIT) method, remedy this by parallelizing across time-steps, and have shown promising results for parabolic problems. However, chaotic problems have proved more difficult, since chaotic initial value problems are inherently ill-conditioned. MGRIT relies on a hierarchy of successively coarser time-grids to iteratively correct the solution on the finest time-grid, but due to the nature of chaotic systems, subtle inaccuracies on the coarser levels can lead to poor coarse-grid corrections. Here we propose a modification to nonlinear FAS multigrid, as well as a novel time-coarsening scheme, which together better capture long term behavior on coarse grids and greatly improve convergence of MGRIT for chaotic initial value problems. We provide supporting numerical results for the Lorenz system model problem.
翻译:由于CPU时钟速度停滞,高性能计算机的核心计数越来越高,因此利用这些新结构需要增加平行性。传统的连续时间总体计划是一个很大的瓶颈,因为许多类型的模拟需要大量的时间步骤,必须按顺序进行计算。同时在时间计划中,如多格减少时间(MGRIT)方法,通过跨时间步骤的平行纠正,并显示出对抛物线问题的有希望的结果。然而,混乱问题证明更为困难,因为混乱的初始值问题本来就是固有的问题。 MGRIT依靠连续粗略的时间网的等级来迭接地纠正最佳时间网的解决方案,但由于混乱系统的性质,粗格的微妙不准确可能会导致粗格纠正。我们在这里建议对非线性FAS多格进行修改,并提出了一个新的时间分解计划,从而更好地捕捉到在粗格网络上的长期行为,大大改进MGRIT系统对混乱初始值问题的趋同。