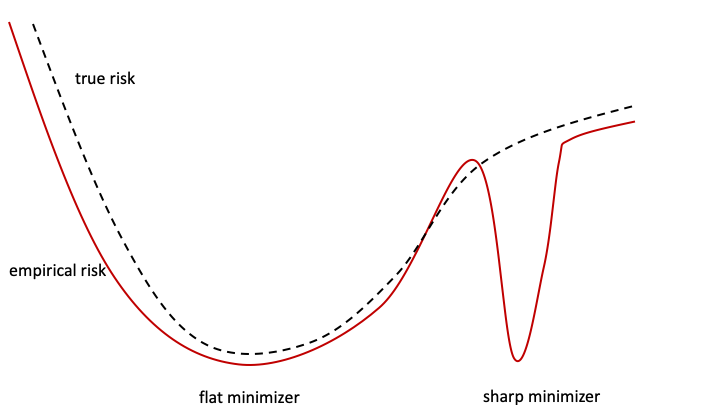
The theoretical and empirical performance of Empirical Risk Minimization (ERM) often suffers when loss functions are poorly behaved with large Lipschitz moduli and spurious sharp minimizers. We propose and analyze a counterpart to ERM called Diametrical Risk Minimization (DRM), which accounts for worst-case empirical risks within neighborhoods in parameter space. DRM has generalization bounds that are independent of Lipschitz moduli for convex as well as nonconvex problems and it can be implemented using a practical algorithm based on stochastic gradient descent. Numerical results illustrate the ability of DRM to find quality solutions with low generalization error in sharp empirical risk landscapes from benchmark neural network classification problems with corrupted labels.
翻译:当损失功能与大型Lipschitz moduli和虚假的锐利最小化器不善处理时,减少风险的理论和经验表现往往会受到影响。我们提议和分析机构风险管理的对应方,称为对称风险最小化(DRM),它考虑到参数空间附近社区最坏的实验风险。DRM具有独立于Lipschitz moduli的通用界限,可以用来处理电流和非电流问题。数字结果表明,DRM有能力找到高质量的解决方案,在与腐败标签有关的基准神经网络分类问题中,在明显的实验风险景观中,发现低一般化错误。