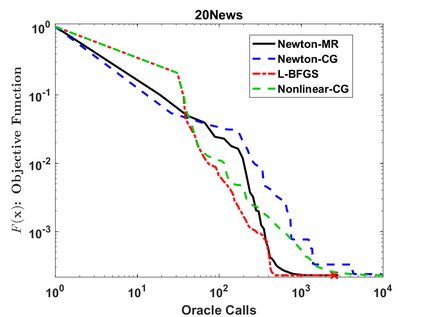
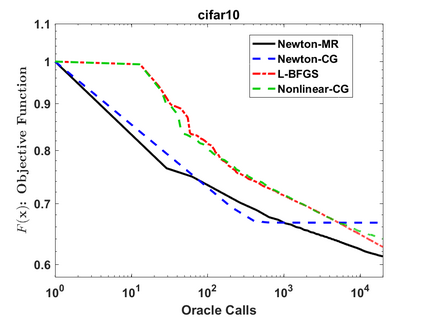
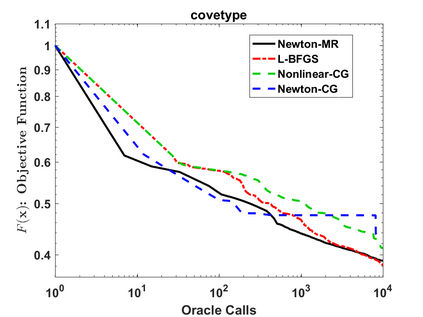
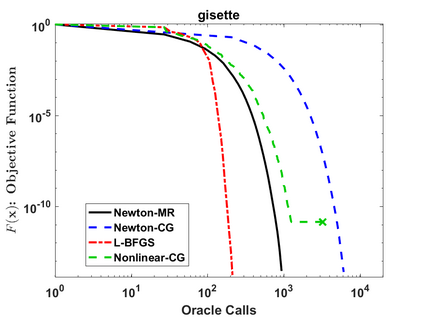
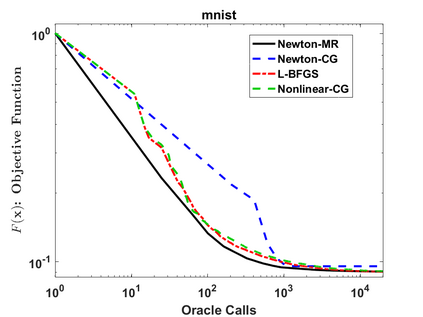
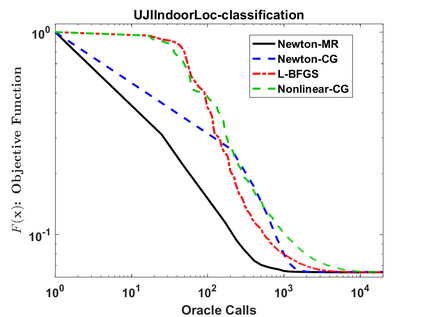
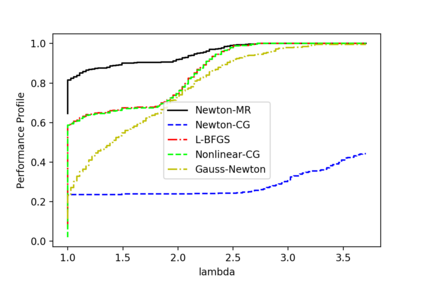
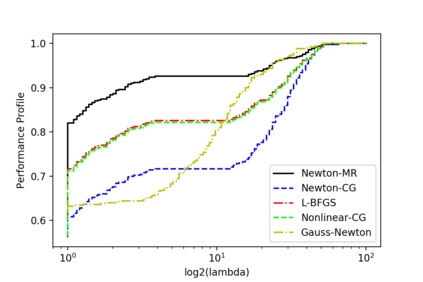
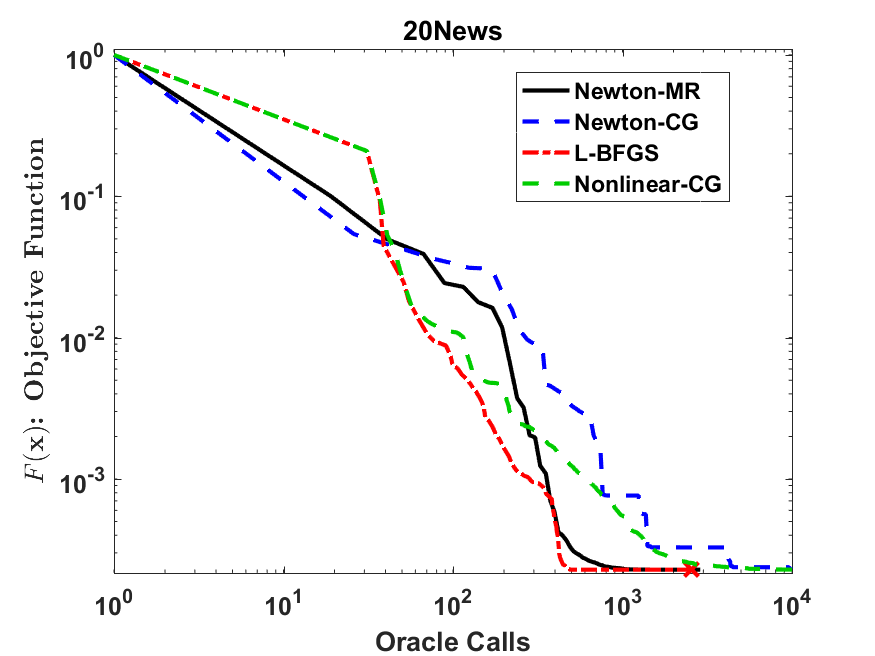
We consider a variant of inexact Newton Method, called Newton-MR, in which the least-squares sub-problems are solved approximately using Minimum Residual method. By construction, Newton-MR can be readily applied for unconstrained optimization of a class of non-convex problems known as invex, which subsumes convexity as a sub-class. For invex optimization, instead of the classical Lipschitz continuity assumptions on gradient and Hessian, Newton-MR's global convergence can be guaranteed under a weaker notion of joint regularity of Hessian and gradient. We also obtain Newton-MR's problem-independent local convergence to the set of minima. We show that fast local/global convergence can be guaranteed under a novel inexactness condition, which, to our knowledge, is much weaker than the prior related works. Numerical results demonstrate the performance of Newton-MR as compared with several other Newton-type alternatives on a few machine learning problems.
翻译:我们考虑的是非精确牛顿方法的变体,即牛顿-MR,其中最不平方的子问题可以使用最低残留法解决。通过建造,牛顿-MR可以很容易地用于不加限制地优化一类非凝固问题,称为Invex,它把同质分解作为一个子类。对于Invex优化,而不是传统的Lipschitz关于梯度和Hessian的连续性假设,牛顿-MR的全球趋同可以在一种较弱的海珊和梯度共同规律概念下得到保障。我们还获得了牛顿-MR与一套迷你马的局部趋同。我们表明,在一个新颖的不精确条件下可以保证快速的本地/全球趋同,据我们所知,这种不灵异状况比先前的相关工作要弱得多。数字结果表明,与几个机器学习问题的其他几个牛顿型替代方法相比,牛顿-MR的性能表现得到了保证。