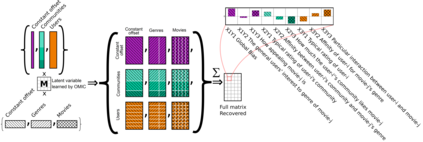
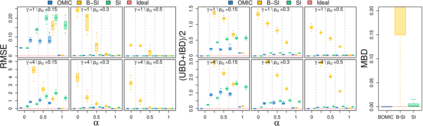
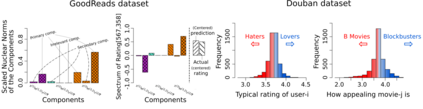
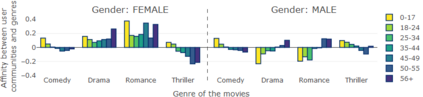
We propose orthogonal inductive matrix completion (OMIC), an interpretable approach to matrix completion based on a sum of multiple orthonormal side information terms, together with nuclear-norm regularization. The approach allows us to inject prior knowledge about the singular vectors of the ground truth matrix. We optimize the approach by a provably converging algorithm, which optimizes all components of the model simultaneously. We study the generalization capabilities of our method in both the distribution-free setting and in the case where the sampling distribution admits uniform marginals, yielding learning guarantees that improve with the quality of the injected knowledge in both cases. As particular cases of our framework, we present models which can incorporate user and item biases or community information in a joint and additive fashion. We analyse the performance of OMIC on several synthetic and real datasets. On synthetic datasets with a sliding scale of user bias relevance, we show that OMIC better adapts to different regimes than other methods. On real-life datasets containing user/items recommendations and relevant side information, we find that OMIC surpasses the state-of-the-art, with the added benefit of greater interpretability.
翻译:我们建议以正反向感应矩阵完成(OMIC),这是一种基于多种正反向侧信息术语和核中枢正规化的总和的可解释的矩阵完成方法。这种方法使我们能够注入关于地面真相矩阵单一矢量的先前知识。我们优化了这种方法,采用了一种可察觉的趋同算法,同时优化模型的所有组成部分。我们研究了我们的方法在无分布分布环境以及在抽样分布中接受统一的边际分布,从而产生学习保证,提高两种情况下注入知识的质量。作为我们框架的特殊情况,我们提出了可以将用户和项目偏见或社区信息纳入共同和添加方式的模式。我们分析了几个合成和真实数据集中的OMIC的性能。在具有用户偏差相关性的合成数据集方面,我们表明OMIC比其他方法更好地适应不同的制度。在包含用户/项目建议和相关侧面信息的实时数据集方面,我们发现OMIC超越了现状,增加了解释性的好处。