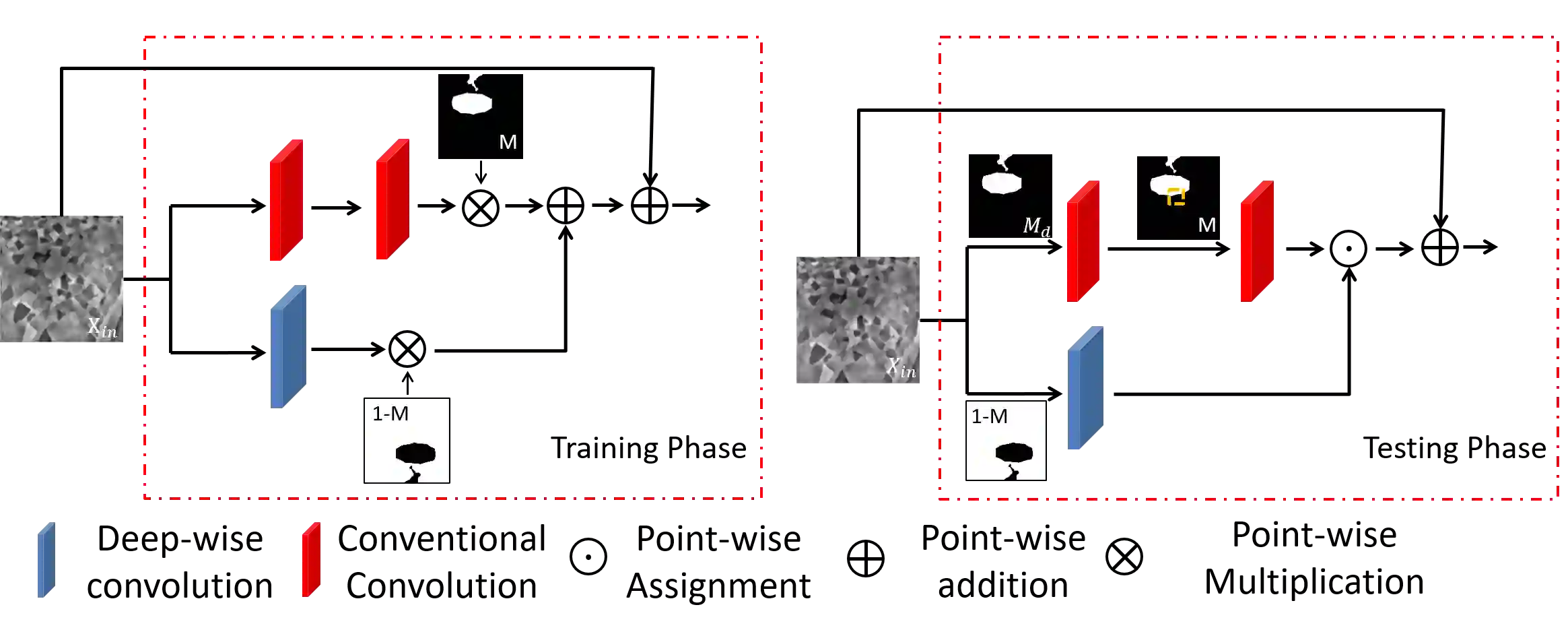
With a wide range of shadows in many collected images, shadow removal has aroused increasing attention since uncontaminated images are of vital importance for many downstream multimedia tasks. Current methods consider the same convolution operations for both shadow and non-shadow regions while ignoring the large gap between the color mappings for the shadow region and the non-shadow region, leading to poor quality of reconstructed images and a heavy computation burden. To solve this problem, this paper introduces a novel plug-and-play Shadow-Aware Dynamic Convolution (SADC) module to decouple the interdependence between the shadow region and the non-shadow region. Inspired by the fact that the color mapping of the non-shadow region is easier to learn, our SADC processes the non-shadow region with a lightweight convolution module in a computationally cheap manner and recovers the shadow region with a more complicated convolution module to ensure the quality of image reconstruction. Given that the non-shadow region often contains more background color information, we further develop a novel intra-convolution distillation loss to strengthen the information flow from the non-shadow region to the shadow region. Extensive experiments on the ISTD and SRD datasets show our method achieves better performance in shadow removal over many state-of-the-arts. Our code is available at https://github.com/xuyimin0926/SADC.
翻译:由于许多收集的图像中有许多阴影,阴影的清除引起了越来越多的关注,因为未受污染的图像对于许多下游多媒体任务至关重要。目前的方法考虑到对影子和非阴影地区的同样颜色绘制作业,而忽略了阴影地区和非阴影地区色彩图绘制之间的巨大差距,导致重建图像质量差和计算负担沉重。为了解决这个问题,本文件引入了一个新型插座和播放的影子-软件动态聚合(SADC)模块,以拆解阴影地区与非阴影地区之间的相互依存关系。受非阴影地区色彩图绘制更易于了解的启发,我们的南共体以计算便宜的方式处理非阴影地区色彩图绘制模块的轻度混凝土区域,并以更复杂的变影模块恢复阴影地区,以确保图像重建的质量。鉴于非阴影地区往往包含更多的背景颜色信息,我们进一步开发了新型的内演化蒸馏损失,以加强非阴影地区与阴影地区之间的信息流动。我们非阴影地区的非阴影区域色彩图图绘制工作以计算便宜的方式处理非阴影区,我们的非阴影区区域,南共体以非阴影区图绘制工作,而我们掌握的STD/Squirodroal ex ex asual ex ex ex ex ex arodududududududududududududustrations