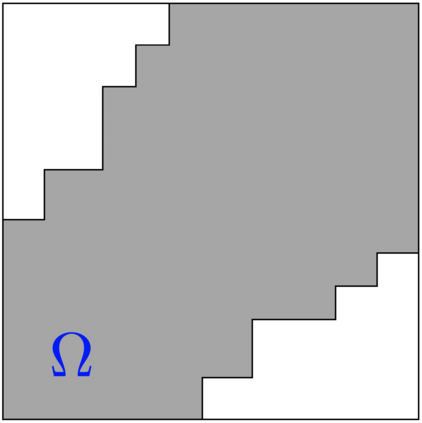
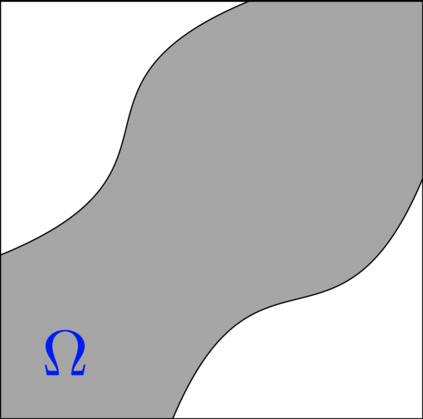
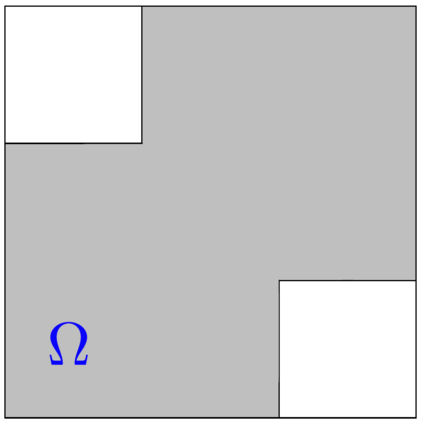
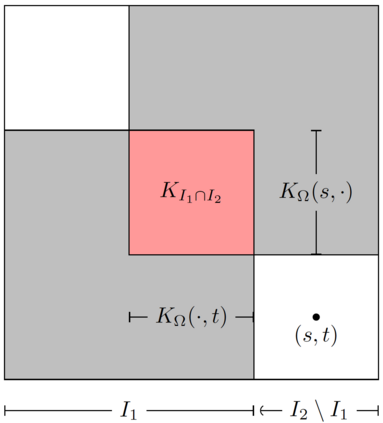
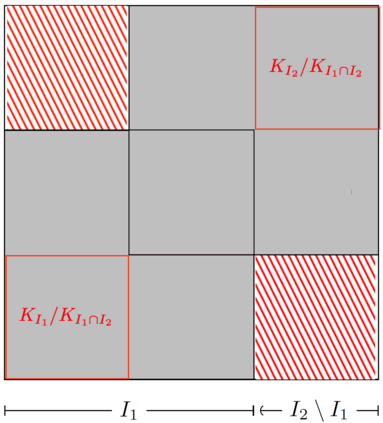
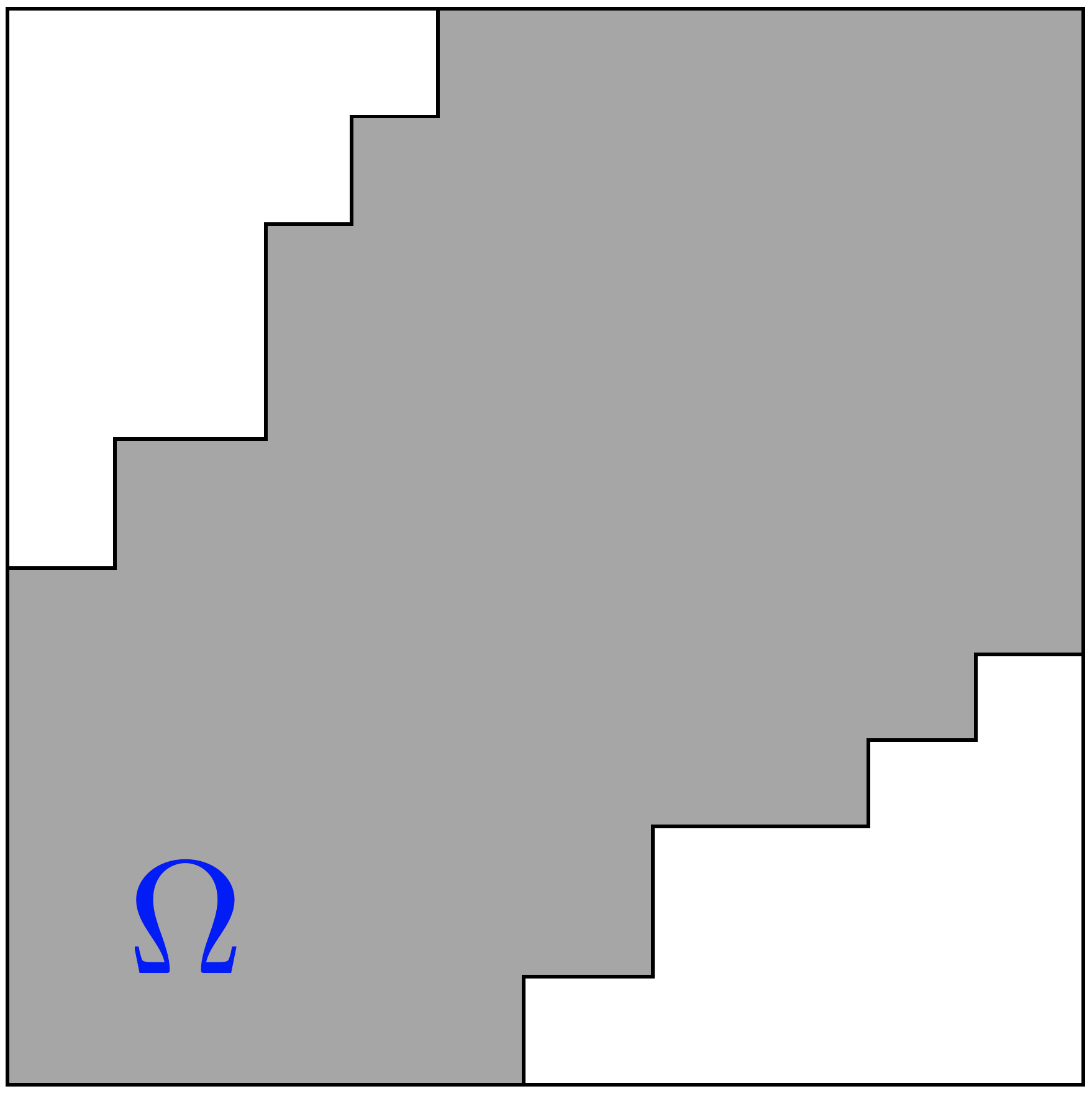
We consider the problem of positive-semidefinite continuation: extending a partially specified covariance kernel from a subdomain $\Omega$ of a domain $I\times I$ to a covariance kernel on the entire domain $I\times I$. For a broad class of domains $\Omega$ called serrated domains, we are able to present a complete theory. Namely, we demonstrate that a canonical completion always exists and can be explicitly constructed. We characterise all possible completions as suitable perturbations of the canonical completion, and determine necessary and sufficient conditions for a unique completion to exist. We interpret the canonical completion via the graphical model structure it induces on the associated Gaussian process. Furthermore, we show how the estimation of the canonical completion reduces to the solution of a system of linear statistical inverse problems in the space of Hilbert-Schmidt operators, and derive rates of convergence under standard source conditions. We conclude by providing extensions of our theory to more general forms of domains.
翻译:我们考虑的是正正正正偏偏继续的问题:将部分指定的共差内核从一个域的分域$\美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=整个域的共差内核。对于一个广泛的域类域 $\ Omega$=美元称为经调整的域,我们可以提出完整的理论。也就是说,我们证明,始终存在一个能够明确构造的完成过程。我们把所有可能的完成描述描述描述为对运河完成过程的适当干扰,并确定独特完成工作的必要和充分条件。我们通过图形模型结构来解释完成的共性完成过程。此外,我们展示了如何通过对古斯进程产生的光学性完成情况进行估计,将缩小到解决希尔-施密特操作者空间线性统计反问题的系统,并在标准源条件下得出趋同率。我们的结论是,将我们的理论扩展为较一般的域。