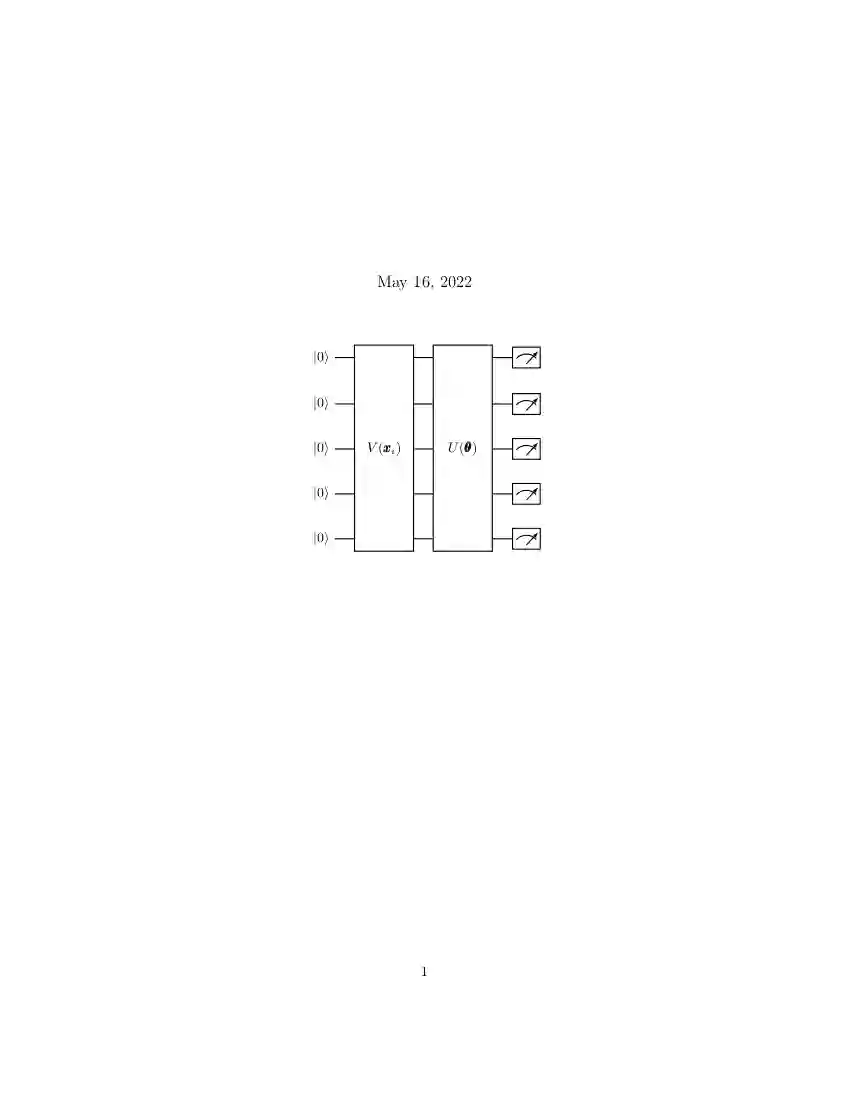
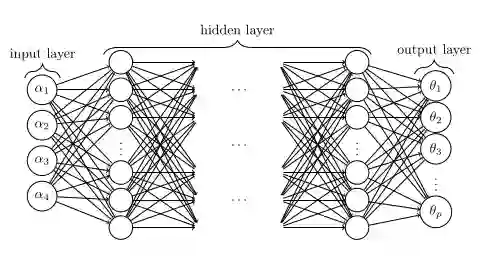
Variational quantum algorithms (VQAs) are among the most promising algorithms in the era of Noisy Intermediate Scale Quantum Devices. The VQAs are applied to a variety of tasks, such as in chemistry simulations, optimization problems, and quantum neural networks. Such algorithms are constructed using a parameterization U($\pmb{\theta}$) with a classical optimizer that updates the parameters $\pmb{\theta}$ in order to minimize a cost function $C$. For this task, in general the gradient descent method, or one of its variants, is used. This is a method where the circuit parameters are updated iteratively using the cost function gradient. However, several works in the literature have shown that this method suffers from a phenomenon known as the Barren Plateaus (BP). This phenomenon is characterized by the exponentially flattening of the cost function landscape, so that the number of times the function must be evaluated to perform the optimization grows exponentially as the number of qubits and parameterization depth increase. In this article, we report on how the use of a classical neural networks in the VQAs input parameters can alleviate the BP phenomenon.
翻译:变化量算算法(VQAs)是新流中间比例量子设备时代最有希望的算法之一。 VQAs应用到化学模拟、优化问题和量子神经网络等各种任务中。这种算法是用一个典型的优化器来构建的,它更新了参数U($\pmb=theta}$),以便最大限度地降低成本函数。对于这项任务,一般而言,使用梯度下降法,或其中的一种变异法。这是电路参数使用成本函数梯度反复更新的方法。然而,文献中的一些作品显示,这种方法受到称为Barren Plateau(BP)的现象的影响。这一现象的特点是成本函数景观急剧平滑,因此,为了进行优化,必须评估该函数的次数会随着Qbits和参数深度的增加而成指数化增长。在本文章中,我们报告如何使用古典神经网络的参数。