Sequential model correction for nonlinear inverse problems

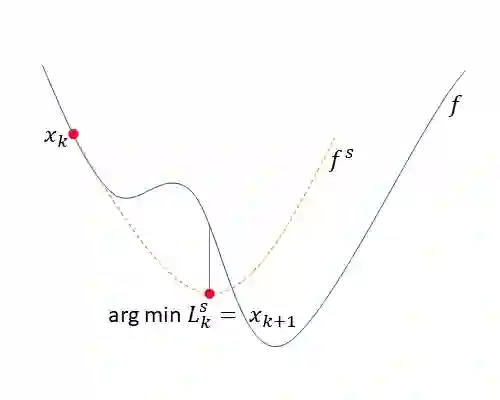
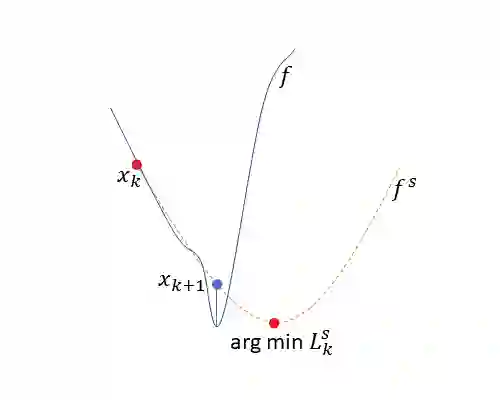
Inverse problems are in many cases solved with optimization techniques. When the underlying model is linear, first-order gradient methods are usually sufficient. With nonlinear models, due to nonconvexity, one must often resort to second-order methods that are computationally more expensive. In this work we aim to approximate a nonlinear model with a linear one and correct the resulting approximation error. We develop a sequential method that iteratively solves a linear inverse problem and updates the approximation error by evaluating it at the new solution. We separately consider cases where the approximation is fixed over iterations and where the approximation is adaptive. In the fixed case we show theoretically under what assumptions the sequence converges. In the adaptive case, particularly considering the special case of approximation by first-order Taylor expansion, we show that the sequence converges to a neighborhood of a local minimizer of the objective function with respect to the exact model. Furthermore, we show that with quadratic objective functions the sequence corresponds to the Gauss-Newton method. Finally, we showcase numerical results superior to the conventional model correction method. We also show, that a fixed approximation can provide competitive results with considerable computational speed-up.