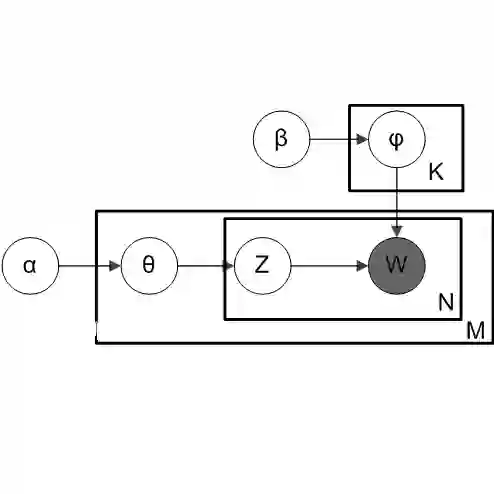
Mixed-membership (MM) models such as Latent Dirichlet Allocation (LDA) have been applied to microbiome compositional data to identify latent subcommunities of microbial species. These subcommunities are informative for understanding the biological interplay of microbes and for predicting health outcomes. However, microbiome compositions typically display substantial cross-sample heterogeneities in subcommunity compositions -- that is, the variability in the proportions of microbes in shared subcommunities across samples -- which is not accounted for in prior analyses. As a result, LDA can produce inference which is highly sensitive to the specification of the number of subcommunities and often divides a single subcommunity into multiple artificial ones. To address this limitation, we incorporate the logistic-tree normal (LTN) model into LDA to form a new MM model. This model allows cross-sample variation in the composition of each subcommunity around some "centroid" composition that defines the subcommunity. Incorporation of auxiliary P\'olya-Gamma variables enables a computationally efficient collapsed blocked Gibbs sampler to carry out Bayesian inference under this model. By accounting for such heterogeneity, our new model restores the robustness of the inference in the specification of the number of subcommunities and allows meaningful subcommunities to be identified.
翻译:混合成员(MM)模型,如Lentant Dirichlet分配(LDA)模型,已应用于微生物成份数据,以确定微生物物种的潜在亚群。这些亚群是了解微生物的生物相互作用和预测健康结果的丰富信息,然而,微生物成份通常在亚群构成中显示大量交叉分布式差异 -- -- 也就是说,在样品之间共有的亚群中,微生物成份比例的变异性 -- -- 这在先前的分析中没有说明。因此,LDA可以产生对亚群数量规格非常敏感的推断,而且往往将一个单一亚群分成多种人。为解决这一问题,我们将物流正常(LTN)模型纳入LDA,形成一个新的MMM模型。这一模型允许每个亚群类组成中一些“中心”组成的交叉分布式变异性,界定了亚群群。将辅助P\'olya-Gamma变量纳入该模型下的计算性能高效的崩溃性,并常常将一个子群分群划分成多种人种。为了解决这一局限性,我们将物流正常的样本模型纳入新的代号。