PAC-Bayesian Learning of Aggregated Binary Activated Neural Networks with Probabilities over Representations

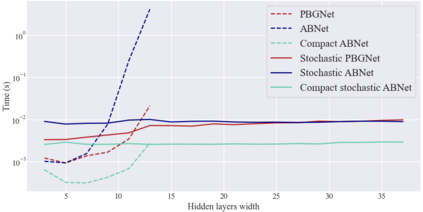
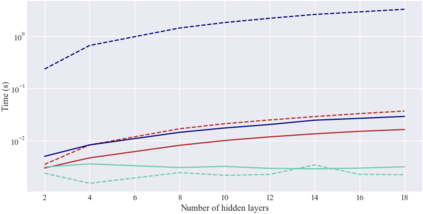
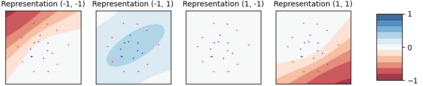
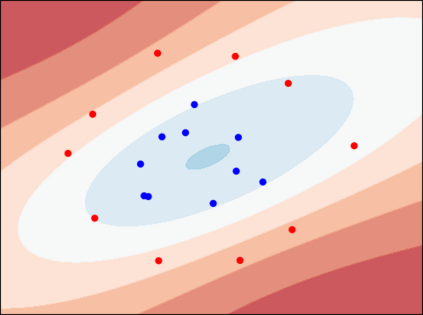
Considering a probability distribution over parameters is known as an efficient strategy to learn a neural network with non-differentiable activation functions. We study the expectation of a probabilistic neural network as a predictor by itself, focusing on the aggregation of binary activated neural networks with normal distributions over real-valued weights. Our work leverages a recent analysis derived from the PAC-Bayesian framework that derives tight generalization bounds and learning procedures for the expected output value of such an aggregation, which is given by an analytical expression. While the combinatorial nature of the latter has been circumvented by approximations in previous works, we show that the exact computation remains tractable for deep but narrow neural networks, thanks to a dynamic programming approach. This leads us to a peculiar bound minimization learning algorithm for binary activated neural networks, where the forward pass propagates probabilities over representations instead of activation values. A stochastic counterpart that scales to wide architectures is proposed.