Time Series Forecasting Using Manifold Learning

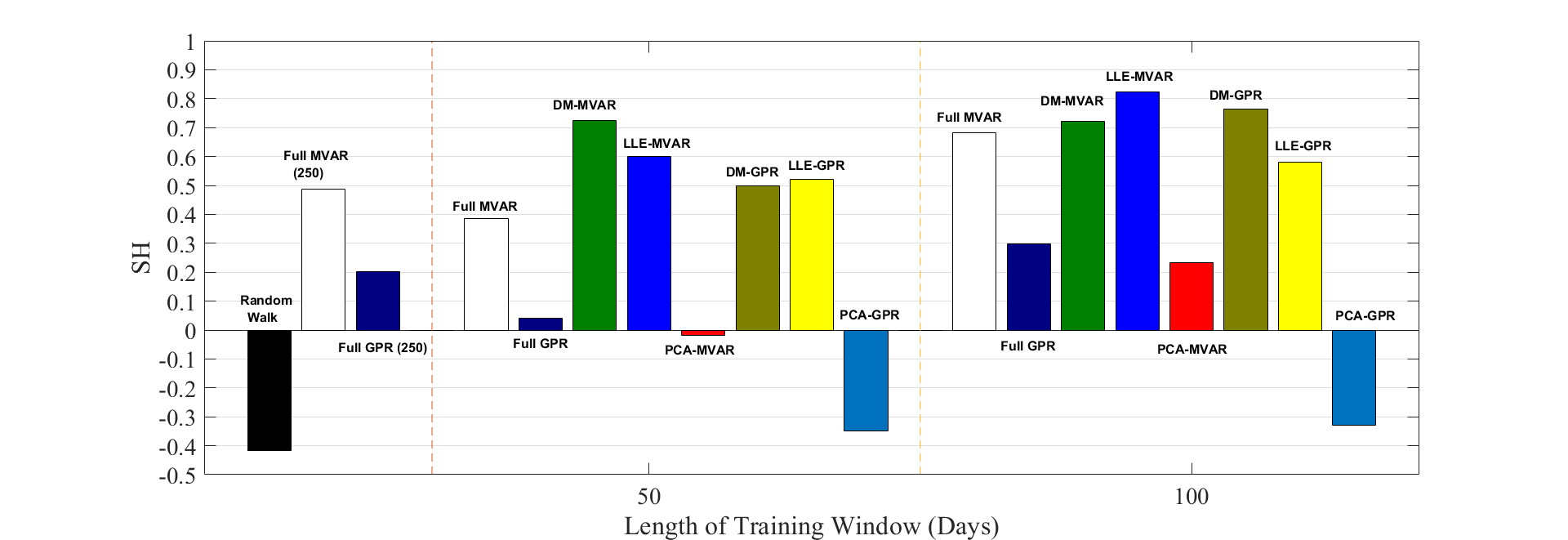
We address a three-tier numerical framework based on manifold learning for the forecasting of high-dimensional time series. At the first step, we embed the time series into a reduced low-dimensional space using a nonlinear manifold learning algorithm such as Locally Linear Embedding and Diffusion Maps. At the second step, we construct reduced-order regression models on the manifold, in particular Multivariate Autoregressive (MVAR) and Gaussian Process Regression (GPR) models, to forecast the embedded dynamics. At the final step, we lift the embedded time series back to the original high-dimensional space using Radial Basis Functions interpolation and Geometric Harmonics. For our illustrations, we test the forecasting performance of the proposed numerical scheme with four sets of time series: three synthetic stochastic ones resembling EEG signals produced from linear and nonlinear stochastic models with different model orders, and one real-world data set containing daily time series of 10 key foreign exchange rates (FOREX) spanning the time period 19/09/2001-29/10/2020. The forecasting performance of the proposed numerical scheme is assessed using the combinations of manifold learning, modelling and lifting approaches. We also provide a comparison with the Principal Component Analysis algorithm as well as with the naive random walk model and the MVAR and GPR models trained and implemented directly in the high-dimensional space.