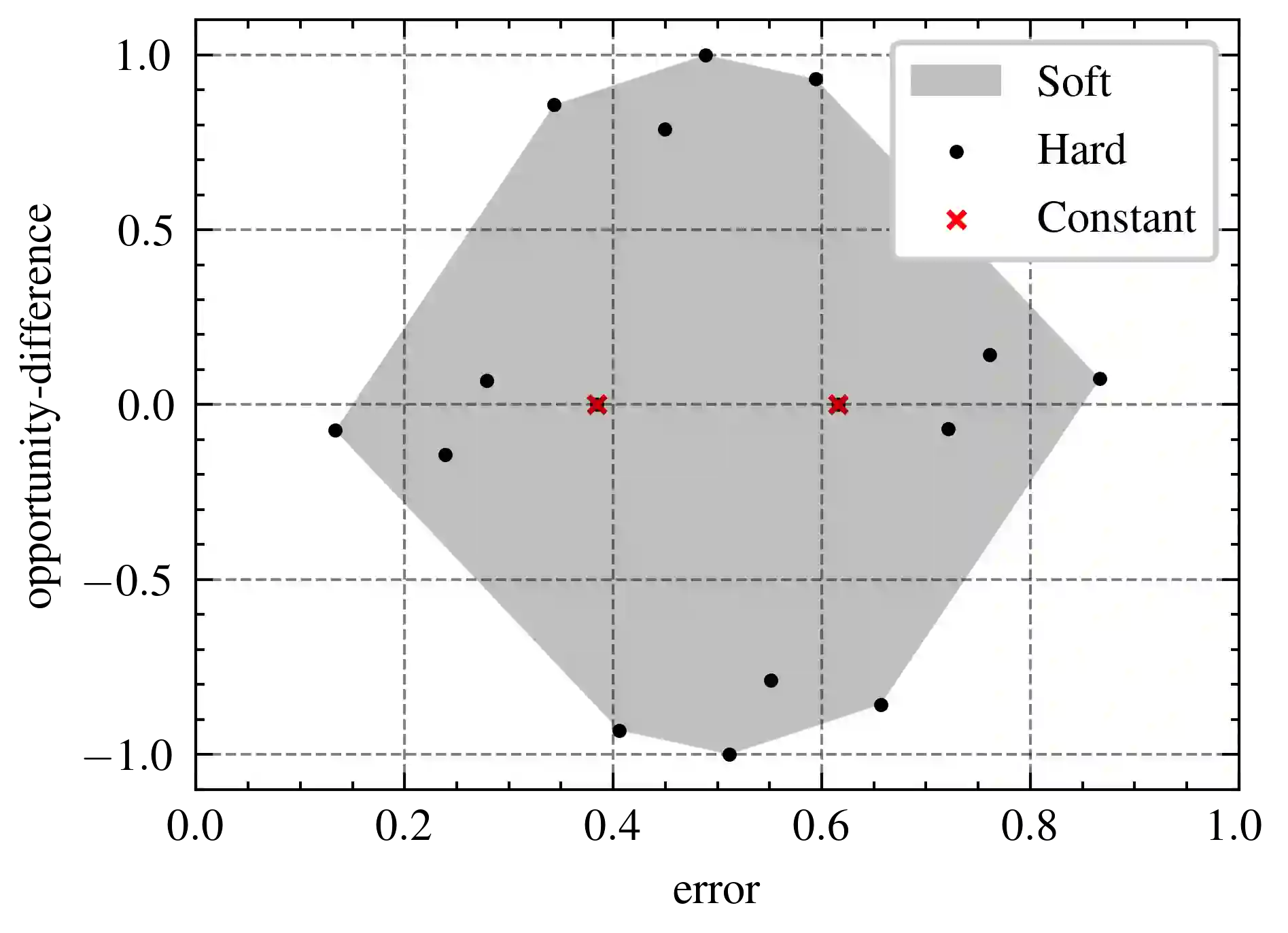
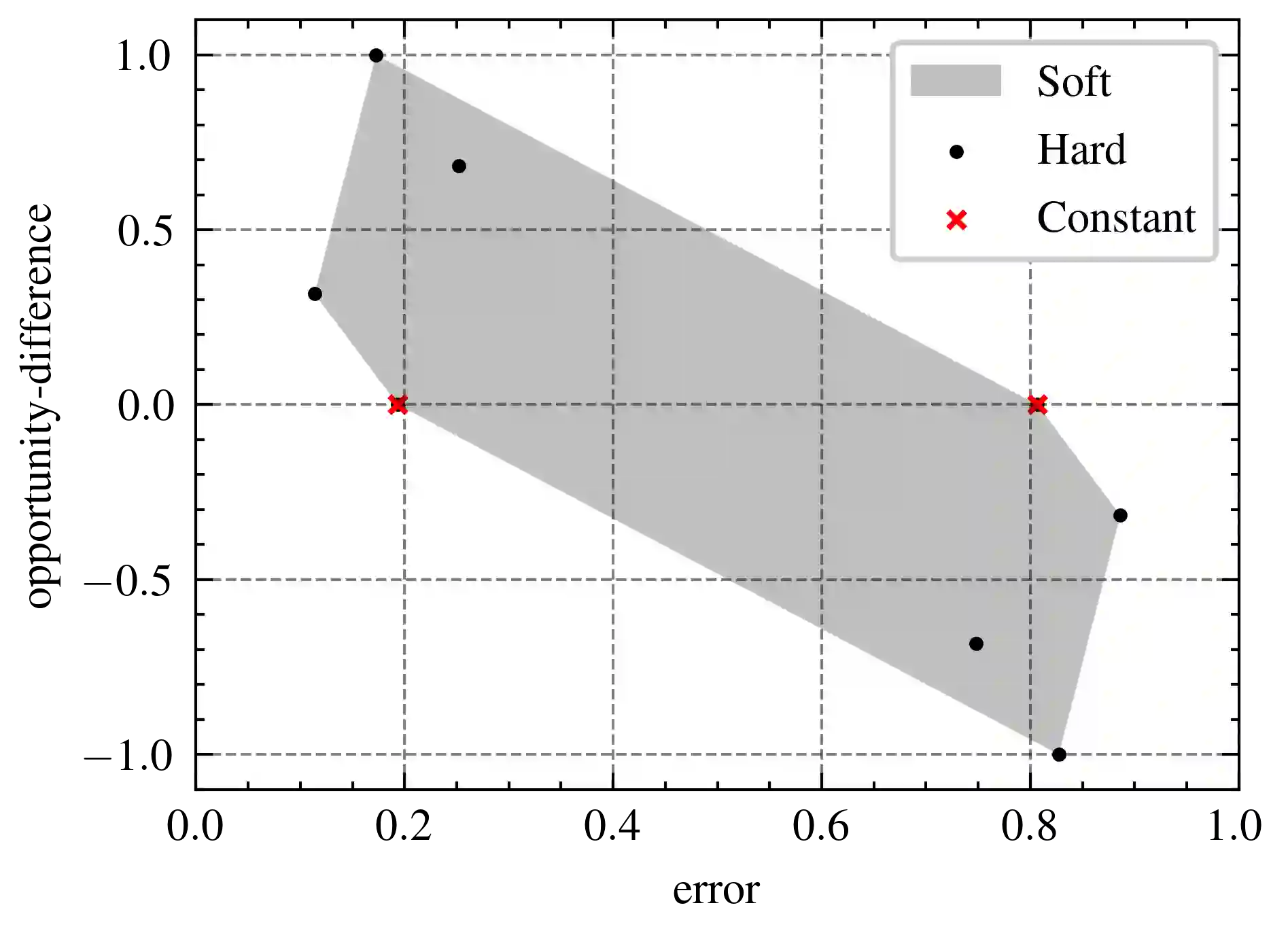
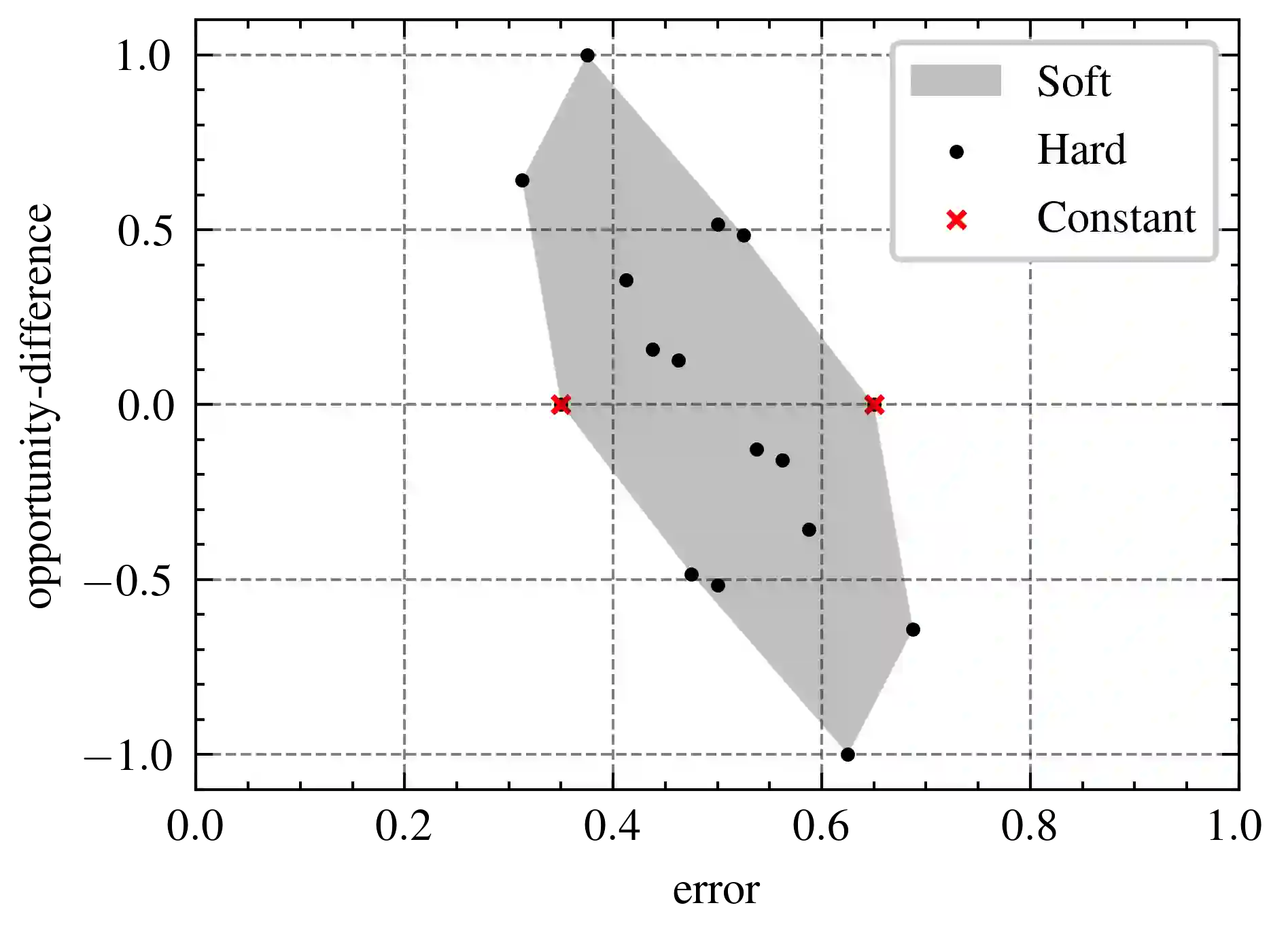
One of the main concerns about fairness in machine learning (ML) is that, in order to achieve it, one may have to trade off some accuracy. To overcome this issue, Hardt et al. proposed the notion of equality of opportunity (EO), which is compatible with maximal accuracy when the target label is deterministic with respect to the input features. In the probabilistic case, however, the issue is more complicated: It has been shown that under differential privacy constraints, there are data sources for which EO can only be achieved at the total detriment of accuracy, in the sense that a classifier that satisfies EO cannot be more accurate than a trivial (i.e., constant) classifier. In our paper we strengthen this result by removing the privacy constraint. Namely, we show that for certain data sources, the most accurate classifier that satisfies EO is a trivial classifier. Furthermore, we study the trade-off between accuracy and EO loss (opportunity difference), and provide a sufficient condition on the data source under which EO and non-trivial accuracy are compatible.
翻译:有关机器学习公平性的主要关切之一是,为了实现这种公平性,人们可能必须权衡某些准确性。为了克服这一问题,Hardt等人提出了机会均等的概念(EO),当目标标签对输入特性具有确定性时,这个概念符合最大准确性。然而,在概率方面,问题更为复杂:已经表明,在不同的隐私限制下,只有完全损害准确性才能实现EO的数据源,即满足EO的分类器不能比微不足道的(即经常)分类器更准确,在我们的文件中,我们通过消除隐私限制来强化这一结果。也就是说,我们表明,对于某些数据源,满足EO的最准确的分类器是一个微不足道的分类器。此外,我们研究了准确性和EO损失(机会差异)之间的权衡,并提供了一种充分的条件,即EO和非三重精确性在数据源上是兼容的。