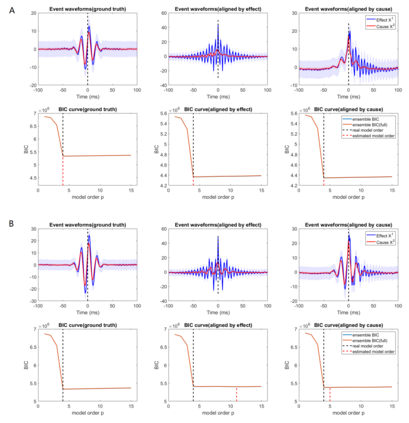
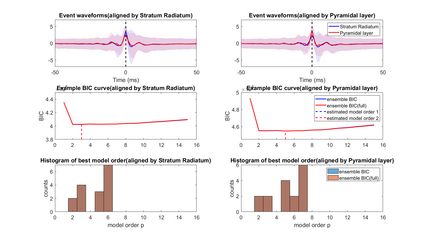
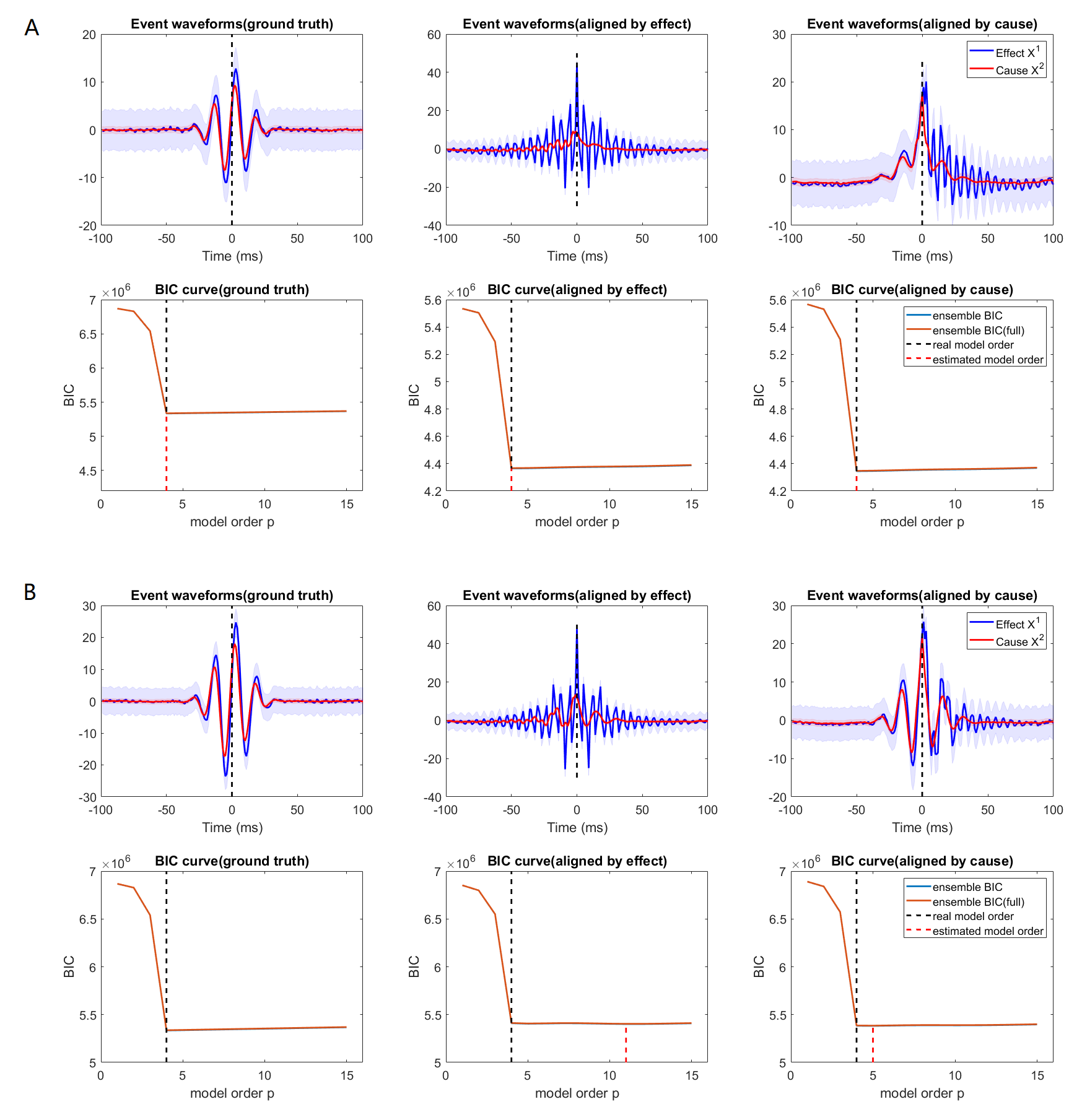
Transient recurring phenomena are ubiquitous in many scientific fields like neuroscience and meteorology. Time inhomogenous Vector Autoregressive Models (VAR) may be used to characterize peri-event system dynamics associated with such phenomena, and can be learned by exploiting multi-dimensional data gathering samples of the evolution of the system in multiple time windows comprising, each associated with one occurrence of the transient phenomenon, that we will call "trial". However, optimal VAR model order selection methods, commonly relying on the Akaike or Bayesian Information Criteria (AIC/BIC), are typically not designed for multi-trial data. Here we derive the BIC methods for multi-trial ensemble data which are gathered after the detection of the events. We show using simulated bivariate AR models that the multi-trial BIC is able to recover the real model order. We also demonstrate with simulated transient events and real data that the multi-trial BIC is able to estimate a sufficiently small model order for dynamic system modeling.
翻译:在神经科学和气象学等许多科学领域,经常反复出现的现象是普遍存在的。时间不相容的矢量自动递减模型(VAR)可用于描述与此类现象相关的近地点系统动态,并且可以通过利用多时间窗口中系统演变的多维数据收集样本来学习,这些样本中每个样本都与短暂现象发生一次有关,我们将称之为“审判”。然而,通常依靠Akaike或Bayesian信息标准(AIC/BIC)的最佳VAR模式订单选择方法通常不是为多位数据设计的。在这里,我们为在探测事件后收集的多位元共振数据绘制了BIC方法。我们用模拟双轨AR模型显示,多位双轨BIC能够恢复真正的模型秩序。我们还用模拟瞬时事件和真实数据证明,多场BIC能够估计一个足够小的动态系统模型。