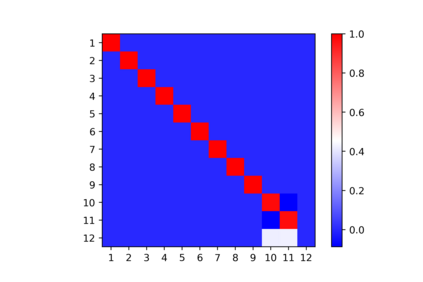
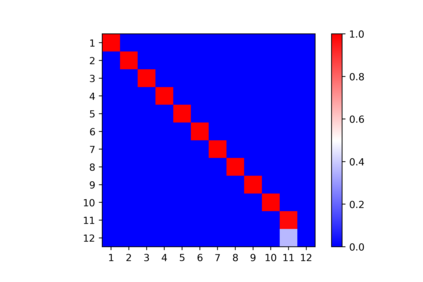
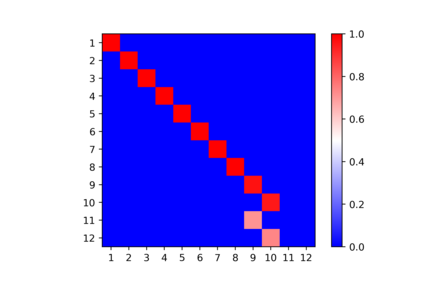
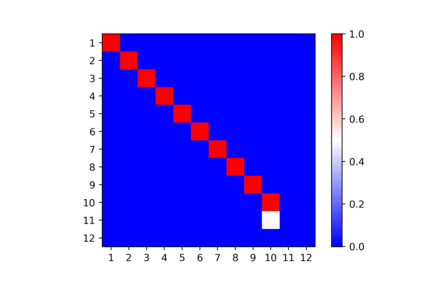
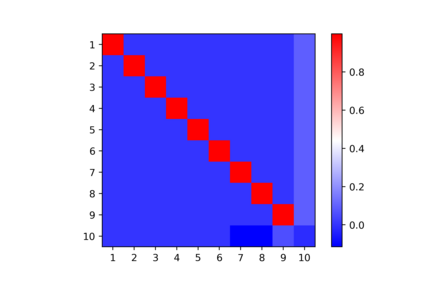
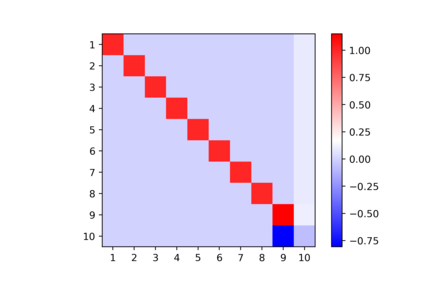
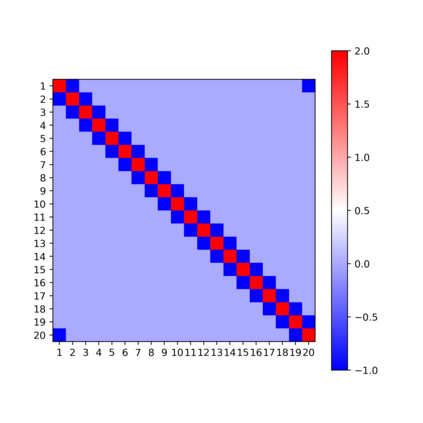
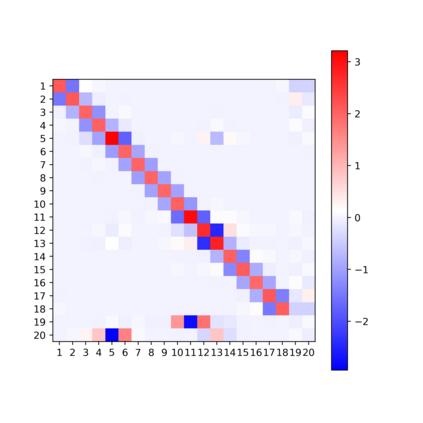
In this note, we consider the highly nonconvex optimization problem associated with computing the rank decomposition of symmetric tensors. We formulate the invariance properties of the loss function and show that critical points detected by standard gradient based methods are \emph{symmetry breaking} with respect to the target tensor. The phenomena, seen for different choices of target tensors and norms, make possible the use of recently developed analytic and algebraic tools for studying nonconvex optimization landscapes exhibiting symmetry breaking phenomena of similar nature.
翻译:暂无翻译
相关内容
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日