Fine spectral analysis of preconditioned matrices and matrix-sequences arising from stage-parallel implicit Runge-Kutta methods of arbitrarily high order

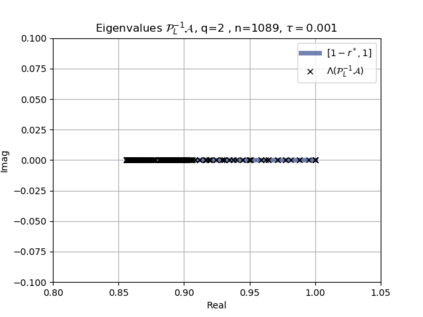
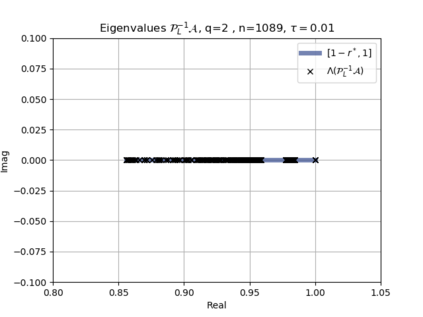
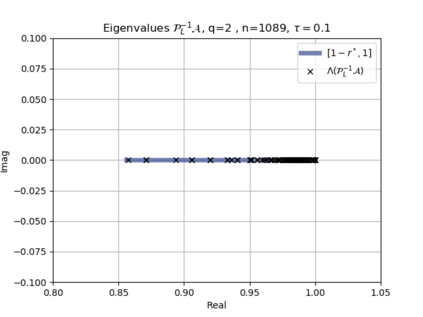
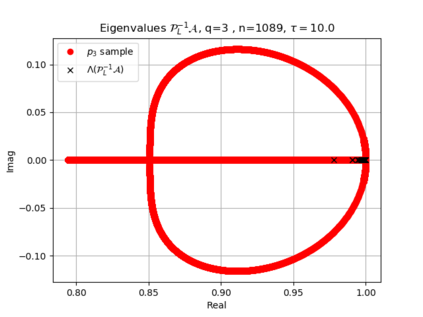
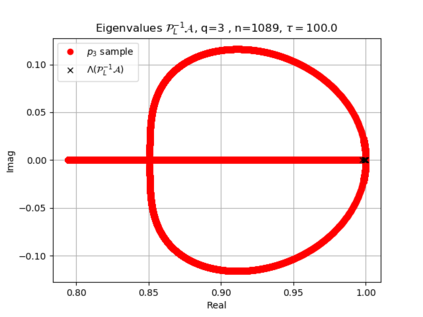
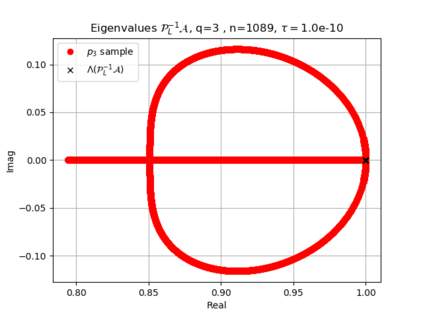
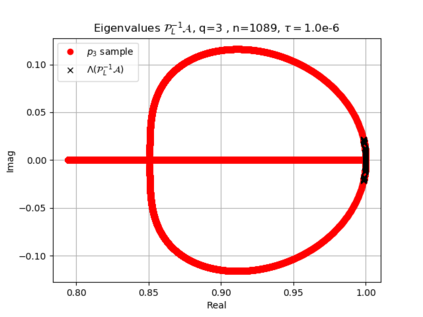
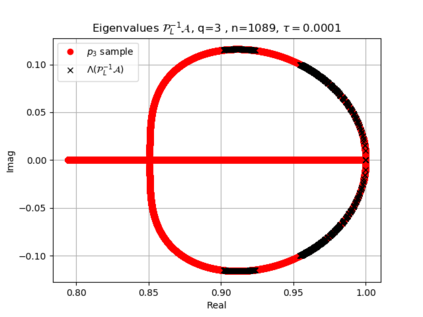
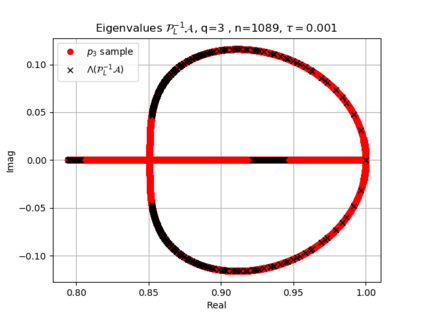
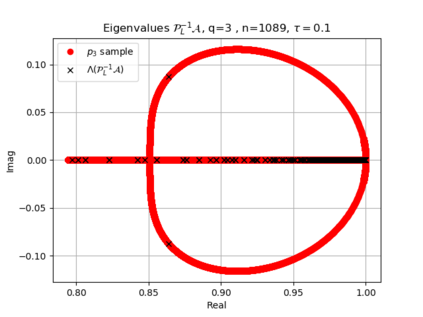
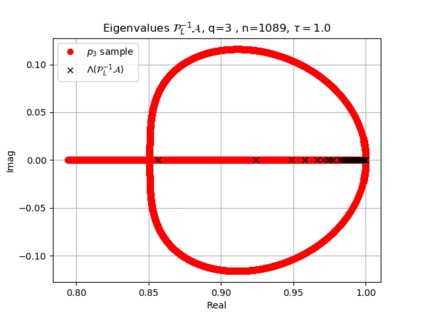
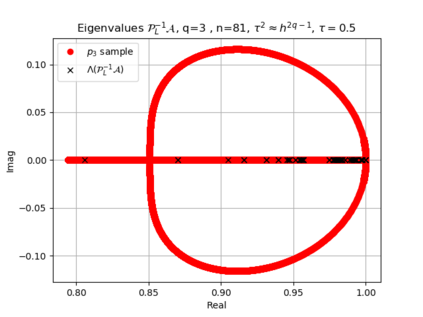
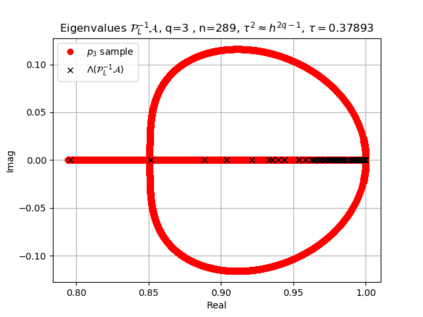
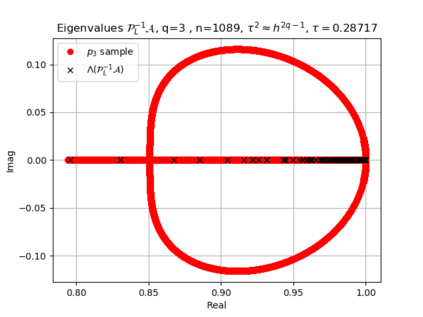
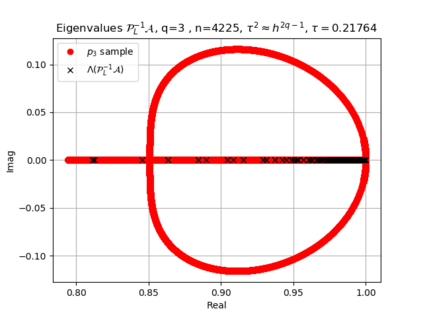
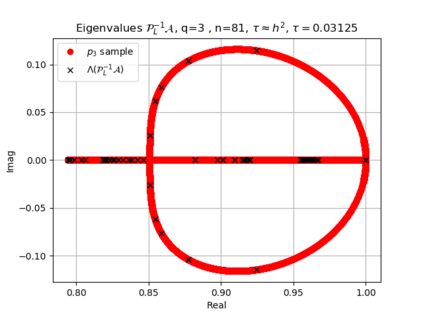
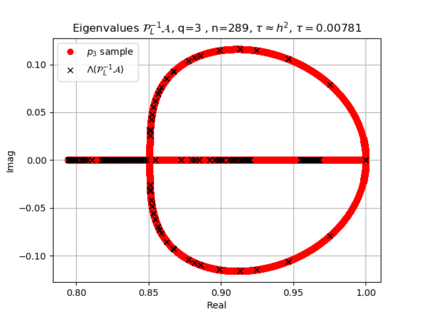
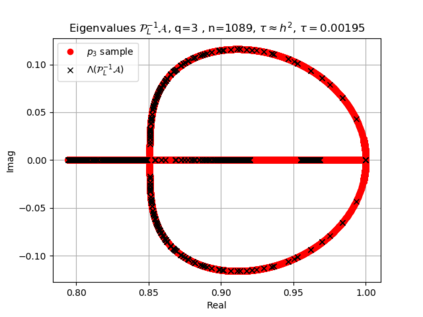
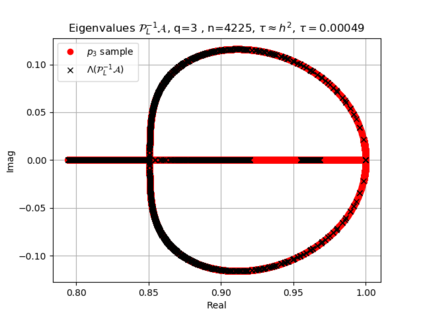
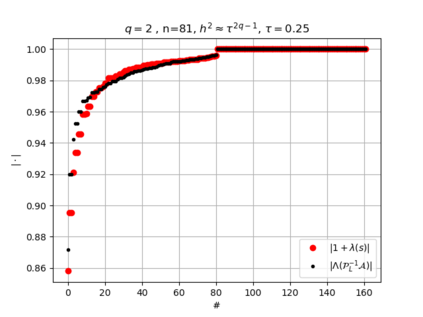
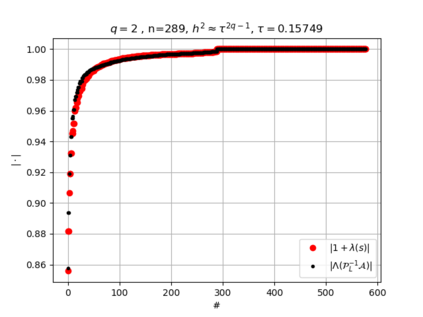
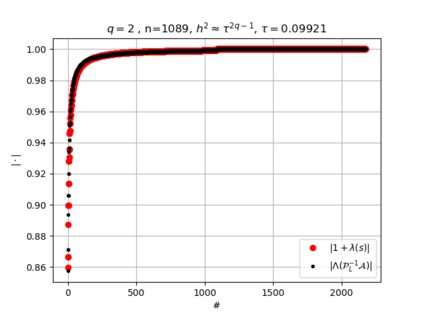
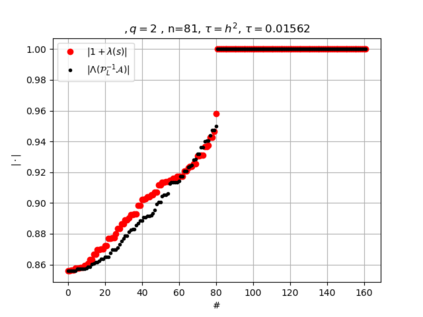
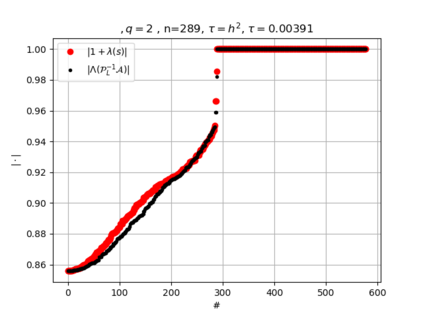
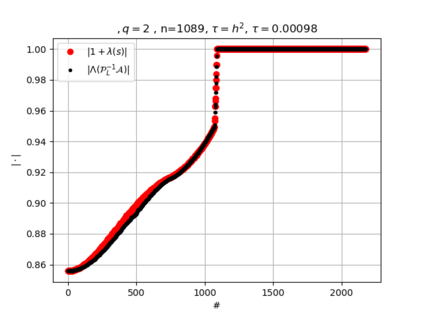
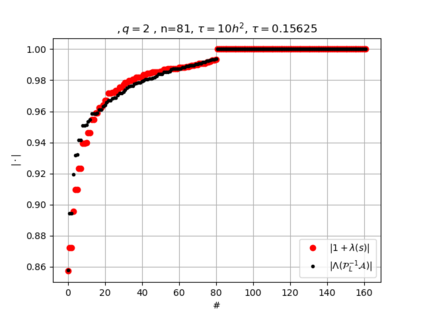
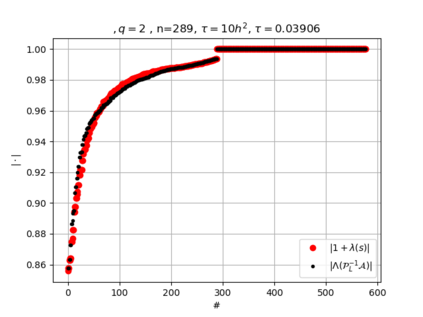
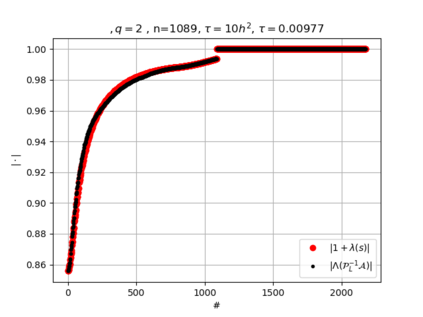
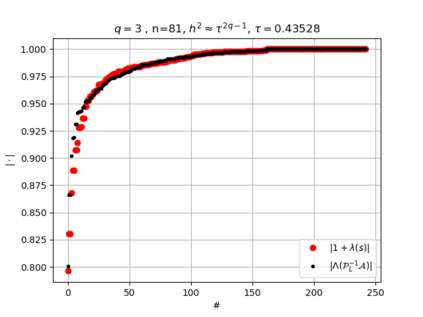
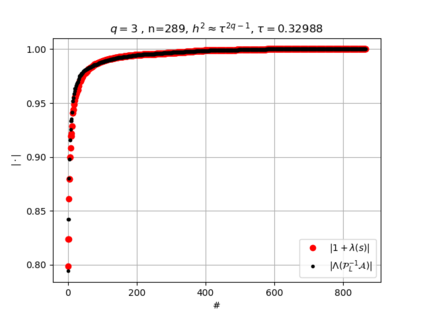
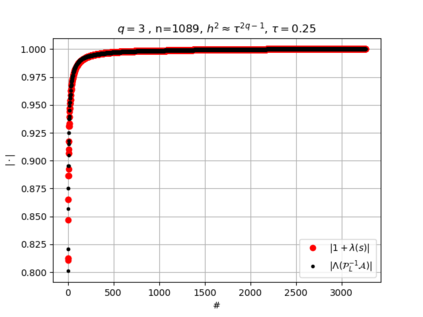
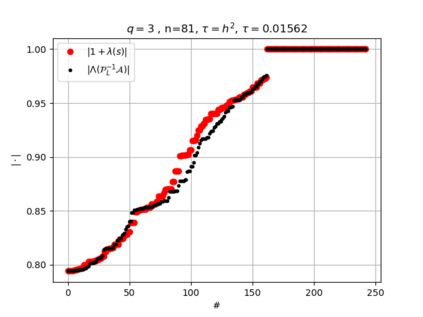
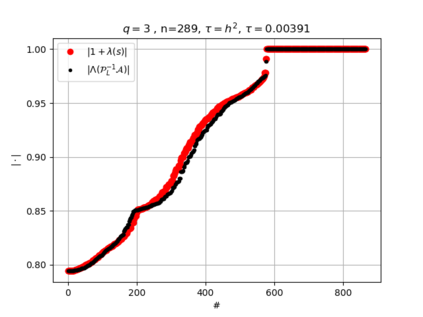
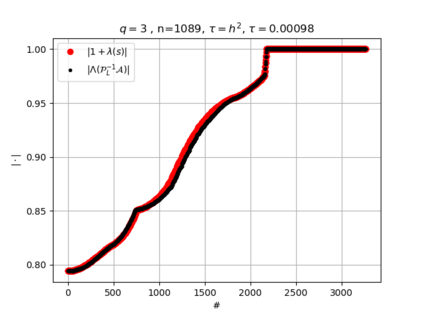
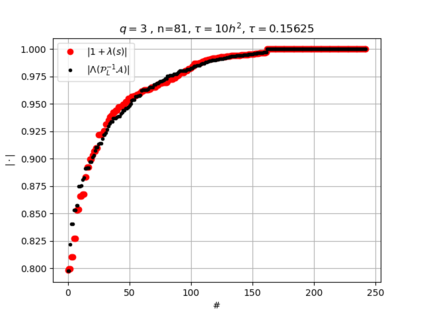
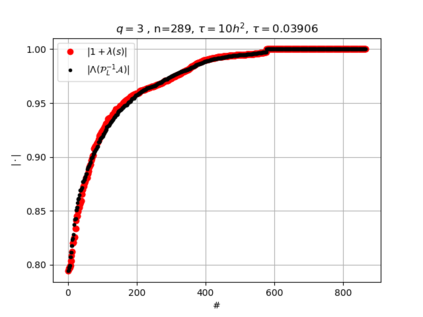
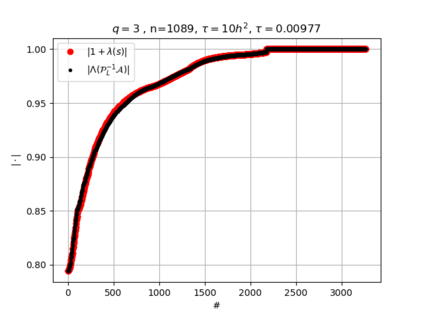
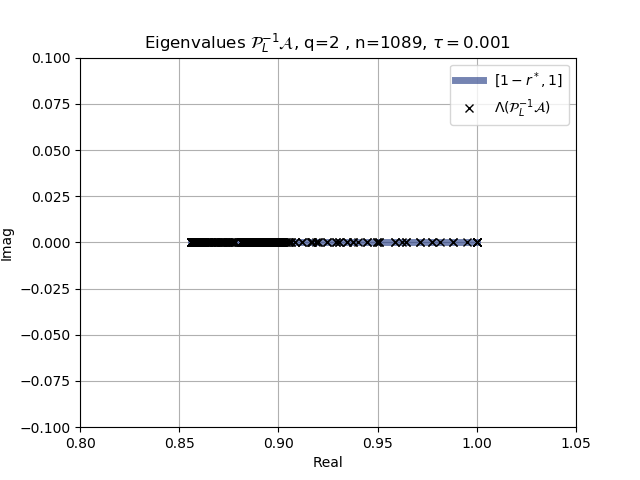
The use of high order fully implicit Runge-Kutta methods is of significant importance in the context of the numerical solution of transient partial differential equations, in particular when solving large scale problems due to fine space resolution with many millions of spatial degrees of freedom and long time intervals. In this study we consider strongly A-stable implicit Runge-Kutta methods of arbitrary order of accuracy, based on Radau quadratures, for which efficient preconditioners have been introduced. A refined spectral analysis of the corresponding matrices and matrix-sequences is presented, both in terms of localization and asymptotic global distribution of the eigenvalues. Specific expressions of the eigenvectors are also obtained. The given study fully agrees with the numerically observed spectral behavior and substantially improves the theoretical studies done in this direction so far. Concluding remarks and open problems end the current work, with specific attention to the potential generalizations of the hereby suggested general approach.