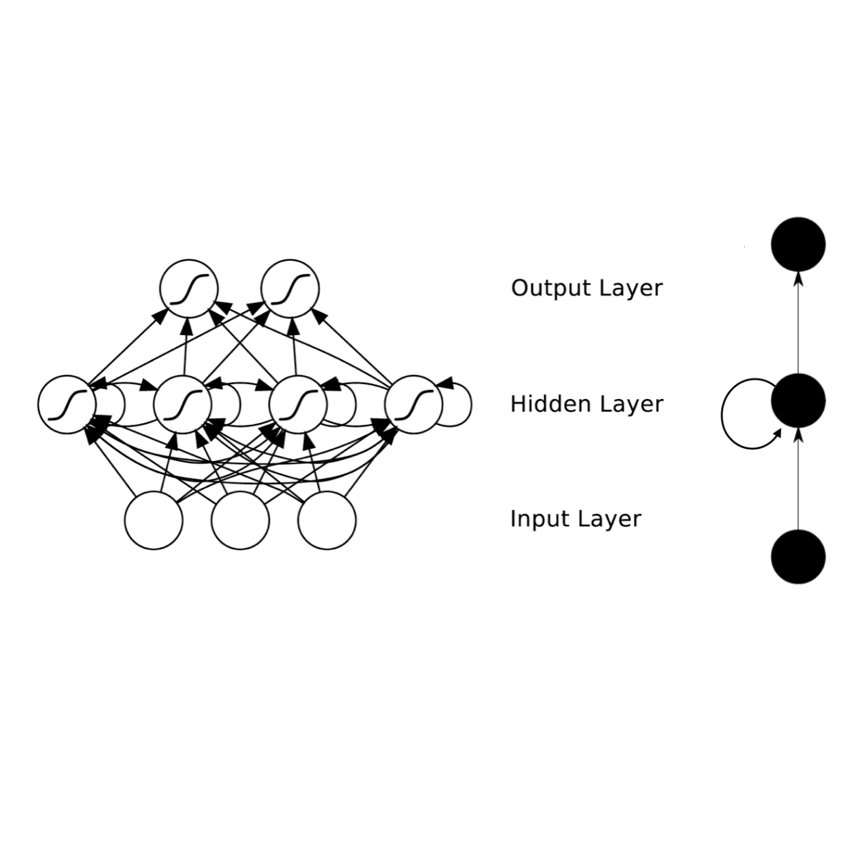
Recurrent neural networks are extremely powerful yet hard to train. One of their issues is the vanishing gradient problem, whereby propagation of training signals may be exponentially attenuated, freezing training. Use of orthogonal or unitary matrices, whose powers neither explode nor decay, has been proposed to mitigate this issue, but their computational expense has hindered their use. Here we show that in the specific case of convolutional RNNs, we can define a convolutional exponential and that this operation transforms antisymmetric or anti-Hermitian convolution kernels into orthogonal or unitary convolution kernels. We explicitly derive FFT-based algorithms to compute the kernels and their derivatives. The computational complexity of parametrizing this subspace of orthogonal transformations is thus the same as the networks' iteration.
翻译:经常神经网络非常强大,但很难训练。 其问题之一是渐渐消失的梯度问题,即培训信号的传播可能会以指数速度减弱,冷冻训练。 已经提出使用正方形或单一矩阵,其功率既不爆炸也不衰减,以缓解这一问题,但其计算成本阻碍了其使用。 这里我们表明,在革命RNN的具体情况下,我们可以定义一个革命指数,而这一操作可以将反对称或反希腊革命核心转换成正向或单一的共变核心。 我们明确地从FFFT中得出计算内核及其衍生物的算法。 因此,使这一次星形变形空间相匹配的计算复杂性与网络的循环相同。