On extension of the data driven ROM inverse scattering framework to partially nonreciprocal arrays

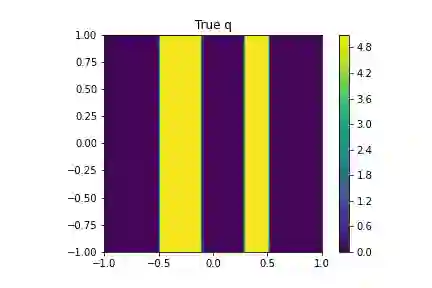
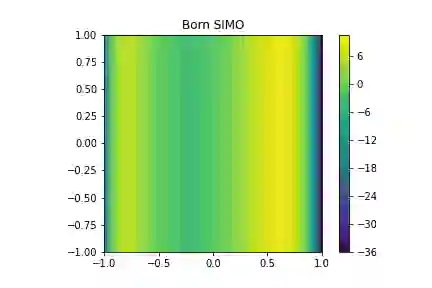
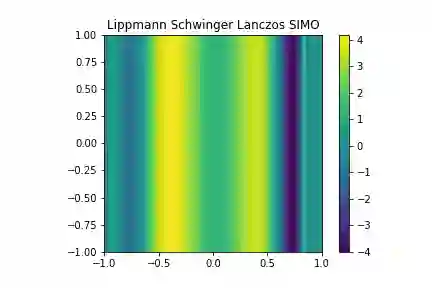
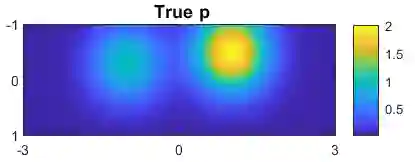
Data-driven reduced order models (ROMs) recently emerged as powerful tool for the solution of inverse scattering problems. The main drawback of this approach is that it was limited to the measurement arrays with reciprocally collocated transmitters and receivers, that is, square symmetric matrix (data) transfer functions. To relax this limitation, we use our previous work [14], where the ROMs were combined with the Lippmann-Schwinger integral equation to produce a direct nonlinear inversion method. In this work we extend this approach to more general transfer functions, including those that are non-symmetric, e.g., obtained by adding only receivers or sources. The ROM is constructed based on the symmetric subset of the data and is used to construct all internal solutions. Remaining receivers are then used directly in the Lippmann-Schwinger equation. We demonstrate the new approach on a number of 1D and 2D examples with non-reciprocal arrays, including a single input/multiple outputs (SIMO) inverse problem, where the data is given by just a single-row matrix transfer function.