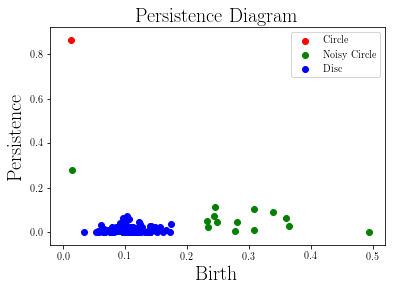
What is the "right" topological invariant of a large point cloud X? Prior research has focused on estimating the full persistence diagram of X, a quantity that is very expensive to compute, unstable to outliers, and far from a sufficient statistic. We therefore propose that the correct invariant is not the persistence diagram of X, but rather the collection of persistence diagrams of many small subsets. This invariant, which we call "distributed persistence," is perfectly parallelizable, more stable to outliers, and has a rich inverse theory. The map from the space of point clouds (with the quasi-isometry metric) to the space of distributed persistence invariants (with the Hausdorff-Bottleneck distance) is a global quasi-isometry. This is a much stronger property than simply being injective, as it implies that the inverse of a small neighborhood is a small neighborhood, and is to our knowledge the only result of its kind in the TDA literature. Moreover, the quasi-isometry bounds depend on the size of the subsets taken, so that as the size of these subsets goes from small to large, the invariant interpolates between a purely geometric one and a topological one. Lastly, we note that our inverse results do not actually require considering all subsets of a fixed size (an enormous collection), but a relatively small collection satisfying certain covering properties that arise with high probability when randomly sampling subsets. These theoretical results are complemented by two synthetic experiments demonstrating the use of distributed persistence in practice.
翻译:X 大点云的“ 右” 表层变量是什么? 先前的研究侧重于估算 X 的完整持续度图, 这个数量对于计算非常昂贵,对于外星来说不稳定,而且远非足够的统计。 因此, 我们建议正确的不变化不是 X 的持久性图, 而是收集许多小子集的持久性图。 这个我们称之为“ 分布性持久性” 的不变化是完全平行的, 更稳定到外部线, 并且具有丰富的反向理论。 从点云空间( 与准测量度测量度) 到分布性持续性实验空间( 与Hausdorf- 博特勒内克距离) 的地图是一个全球性的准测量度图。 这比仅仅具有预测性的多得多的属性, 因为它意味着小邻居的反面是一个小区, 是我们在TDA 文献中唯一的补充结果。 此外, 从点云( 准测量度度测量度测量度测量度测量度测量量) 到分布性持续度空间的空间( ) 是一个非常小的地图, 因此, 我们的精确度的精确度 需要从一个层次的大小 从一个直径的层次到一个层次中, 。