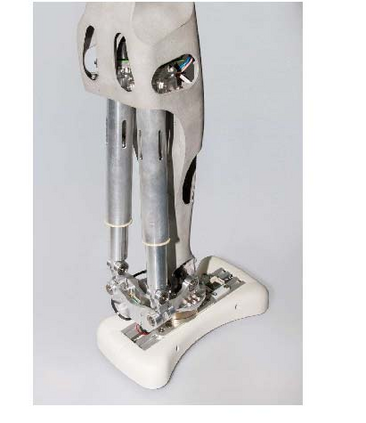
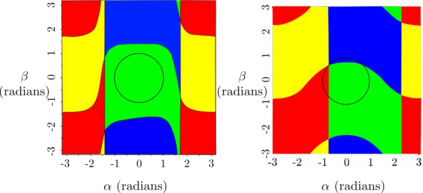
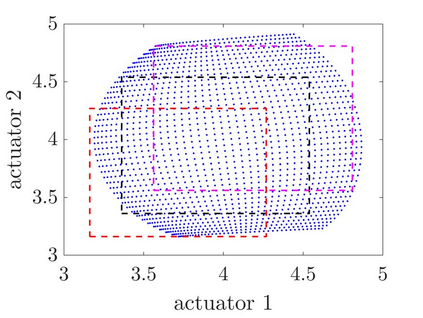
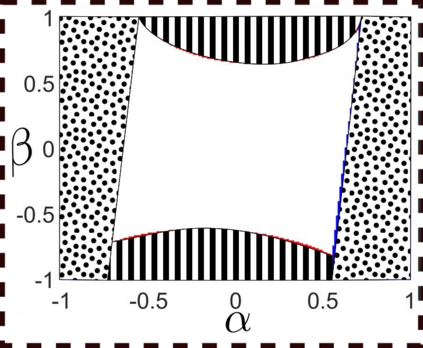
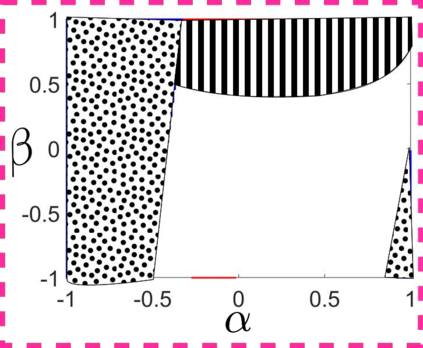
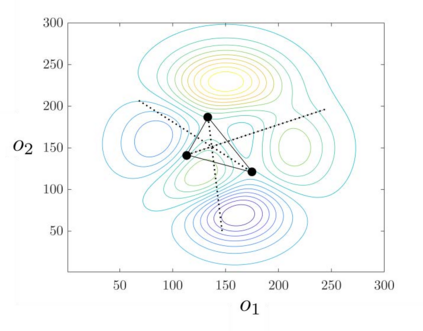
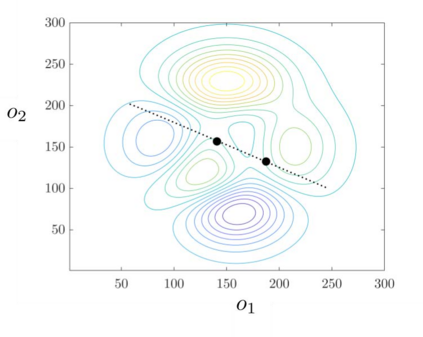
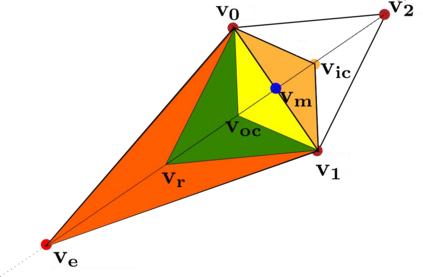
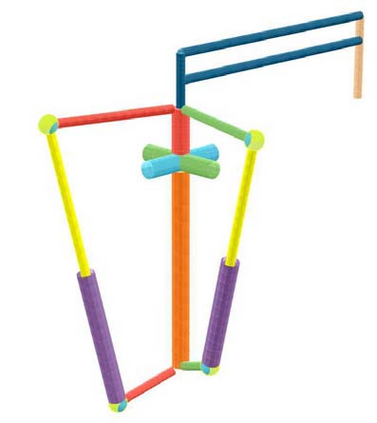
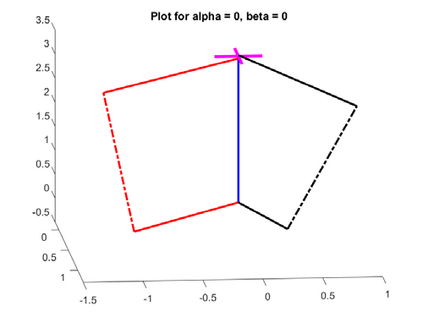
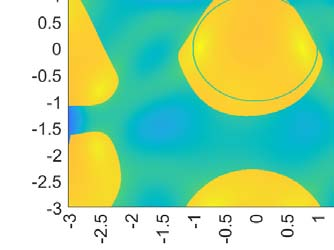
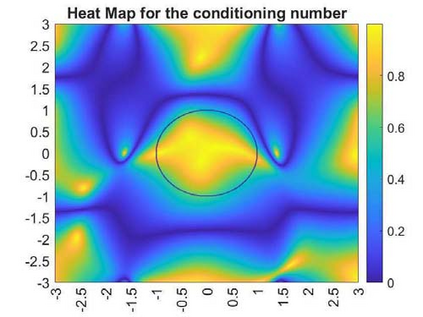
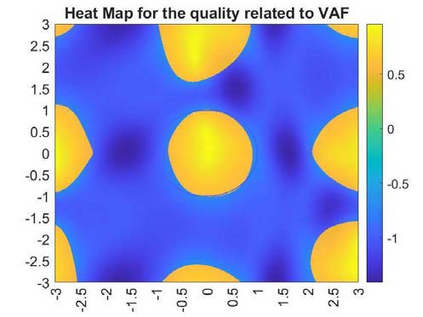
The optimization of parallel kinematic manipulators (PKM) involve several constraints that are difficult to formalize, thus making optimal synthesis problem highly challenging. The presence of passive joint limits as well as the singularities and self-collisions lead to a complicated relation between the input and output parameters. In this article, a novel optimization methodology is proposed by combining a local search, Nelder-Mead algorithm, with global search methodologies such as low discrepancy distribution for faster and more efficient exploration of the optimization space. The effect of the dimension of the optimization problem and the different constraints are discussed to highlight the complexities of closed-loop kinematic chain optimization. The work also presents the approaches used to consider constraints for passive joint boundaries as well as singularities to avoid internal collisions in such mechanisms. The proposed algorithm can also optimize the length of the prismatic actuators and the constraints can be added in modular fashion, allowing to understand the impact of given criteria on the final result. The application of the presented approach is used to optimize two PKMs of different degrees of freedom.
翻译:同步运动操纵器(PKM)的优化涉及若干难以正式确定的制约因素,从而使得最佳组合问题具有高度挑战性; 存在被动联合限制以及单点和自相残杀导致输入参数和输出参数之间的关系复杂; 本条建议采用新的优化方法,将本地搜索、Nelder-Mead算法与全球搜索方法(如为更快、更高效地探索优化空间而进行低差异分布法)相结合,以更快、更高效地探索优化空间; 讨论优化问题层面和不同制约的影响,以突出封闭式流动链优化的复杂性; 工作还介绍了用于考虑被动联合边界制约以及避免此类机制内部碰撞的单一性的方法; 拟议的算法还可以优化典型驱动器的长度和限制,以模块方式添加,以便了解特定标准对最终结果的影响; 采用介绍的方法优化两个不同自由度的PKMs。