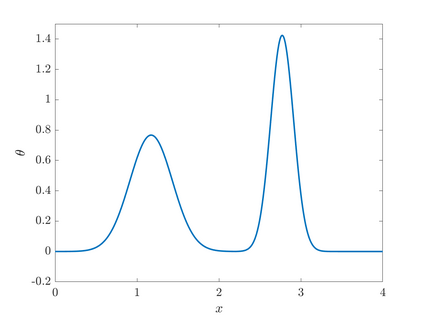
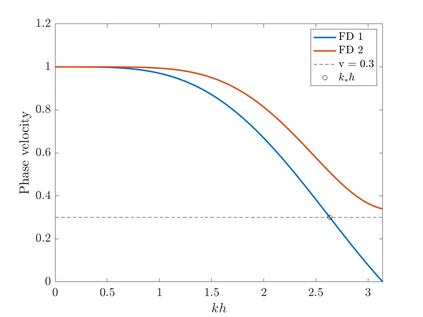
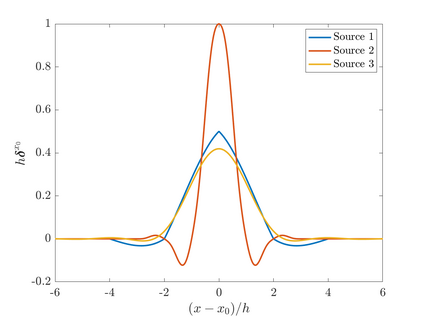
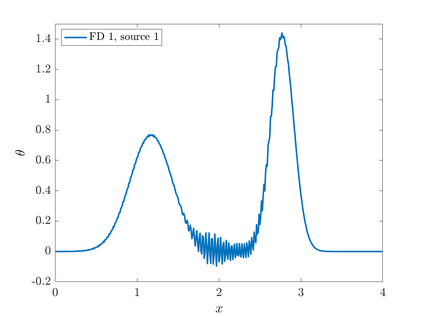
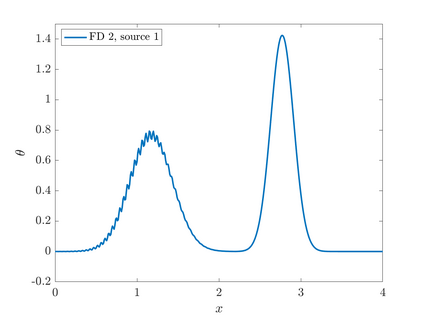
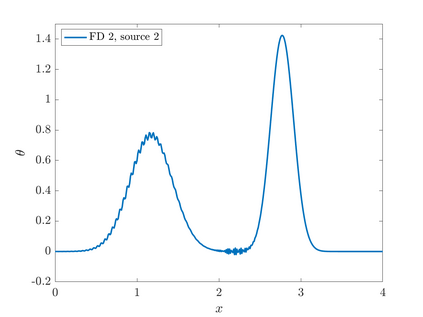
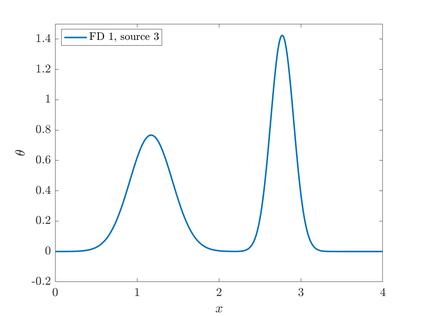
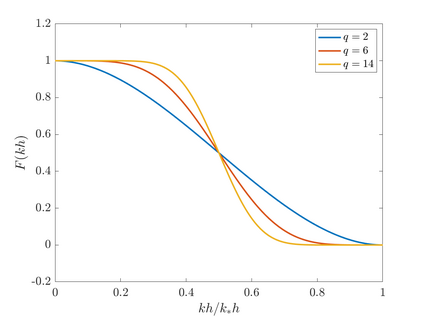
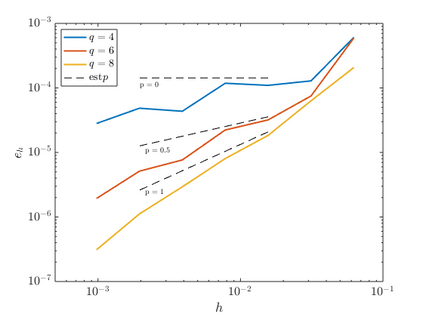
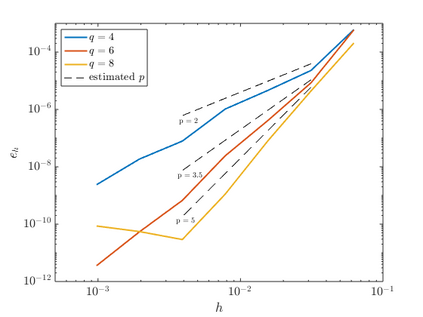
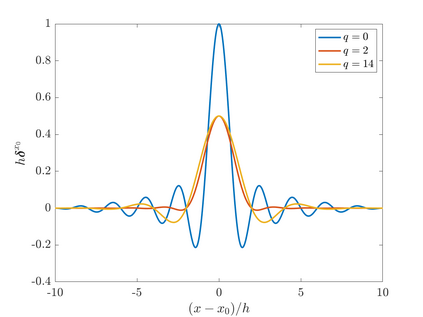
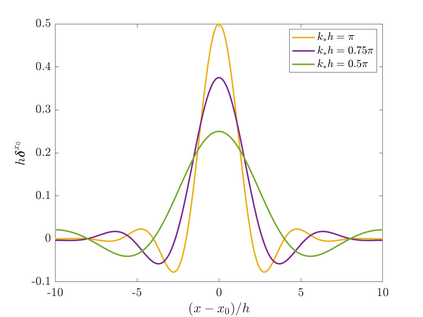
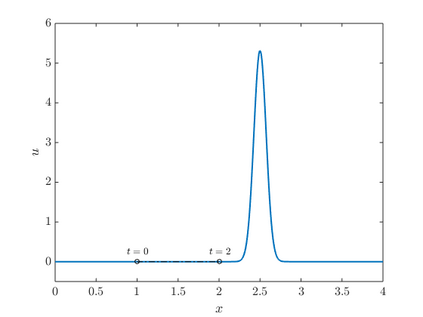
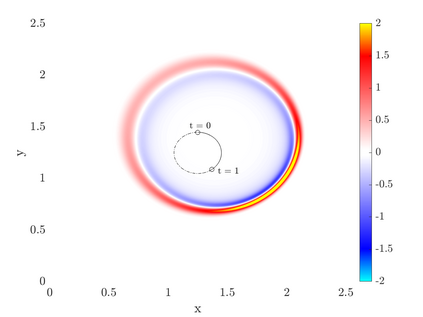
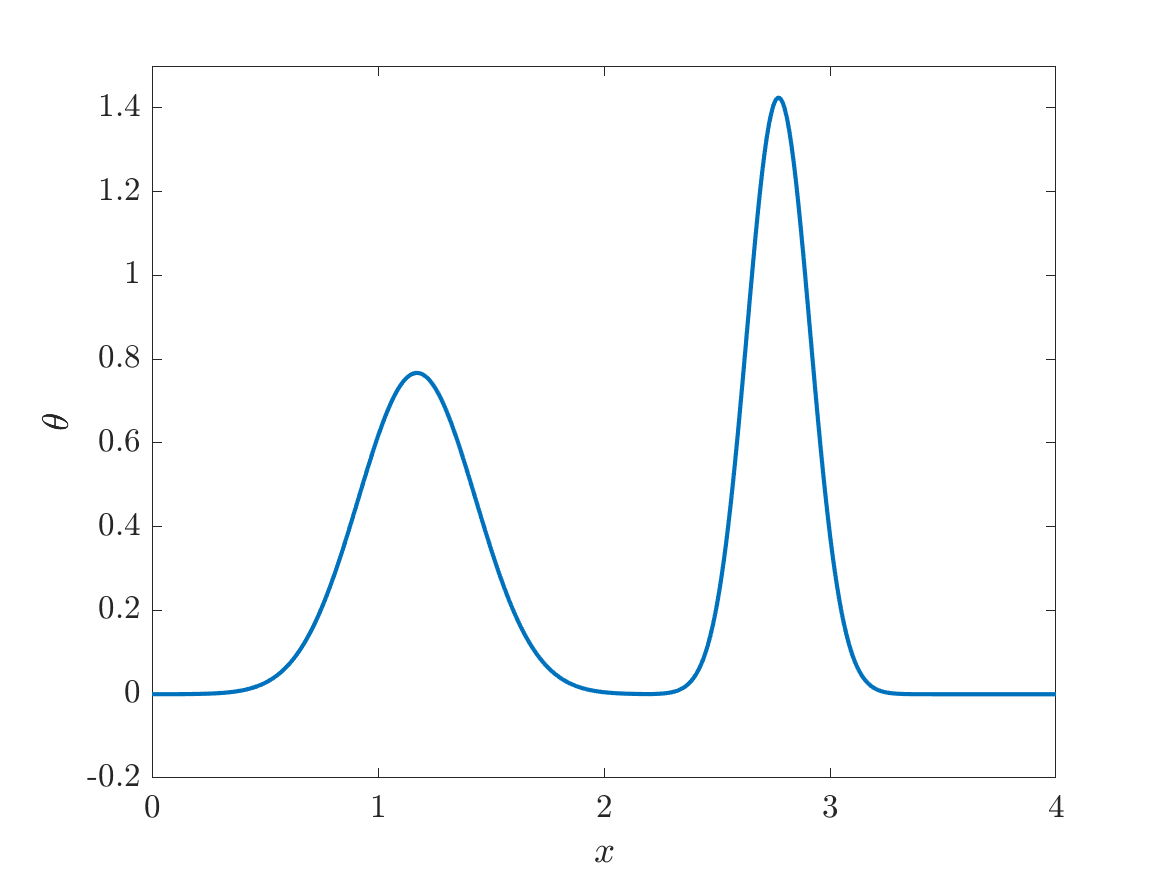
We consider point sources in hyperbolic equations discretized by finite differences. If the source is stationary, appropriate source discretization has been shown to preserve the accuracy of the finite difference method. Moving point sources, however, pose two challenges that do not appear in the stationary case. First, the discrete source must not excite modes that propagate with the source velocity. Second, the discrete source spectrum amplitude must be independent of the source position. We derive a source discretization that meets these requirements and prove design-order convergence of the numerical solution for the one-dimensional advection equation. Numerical experiments indicate design-order convergence also for the acoustic wave equation in two dimensions. The source discretization covers on the order of $\sqrt{N}$ grid points on an $N$-point grid and is applicable for source trajectories that do not touch domain boundaries.
翻译:我们考虑双曲方程式中的点源,并用有限的差异分解。如果源是固定的,则适当的源分解已被证明可以保持有限差异法的准确性。移动点源提出了固定情况下没有出现的两个挑战。首先,离点源不得与源速度相传播的刺激模式相容。第二,离源源频谱振幅必须独立于源位置。我们得出一个符合这些要求的源分解,并证明单维对流方程式的数字解决方案在设计-顺序上的趋同。数字实验表明声波方程式在两个维度上的设计-顺序趋同。源分解范围以$\sqrt{N}为单位,适用于不触动域边界的源轨。