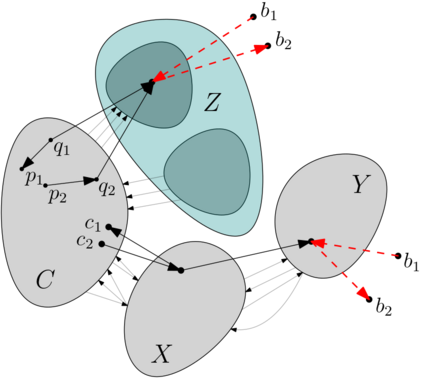
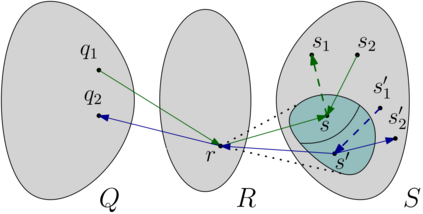
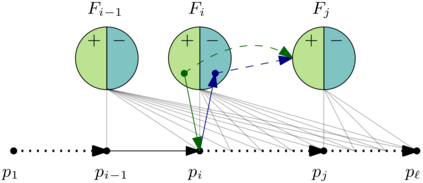
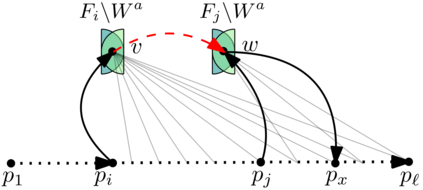
An oriented graph is a digraph that does not contain a directed cycle of length two. An (oriented) graph $D$ is $H$-free if $D$ does not contain $H$ as an induced sub(di)graph. The Gy\'arf\'as-Sumner conjecture is a widely-open conjecture on simple graphs, which states that for any forest $F$, there is some function $f$ such that every $F$-free graph $G$ with clique number $\omega(G)$ has chromatic number at most $f(\omega(G))$. Aboulker, Charbit, and Naserasr [Extension of Gy\'arf\'as-Sumner Conjecture to Digraphs; E-JC 2021] proposed an analogue of this conjecture to the dichromatic number of oriented graphs. The dichromatic number of a digraph $D$ is the minimum number of colors required to color the vertex set of $D$ so that no directed cycle in $D$ is monochromatic. Aboulker, Charbit, and Naserasr's $\overrightarrow{\chi}$-boundedness conjecture states that for every oriented forest $F$, there is some function $f$ such that every $F$-free oriented graph $D$ has dichromatic number at most $f(\omega(D))$, where $\omega(D)$ is the size of a maximum clique in the graph underlying $D$. In this paper, we perform the first step towards proving Aboulker, Charbit, and Naserasr's $\overrightarrow{\chi}$-boundedness conjecture by showing that it holds when $F$ is any orientation of a path on four vertices.
翻译:方向图形是一个不包含直截面长度周期的绘图。 一个( 面向的) 图形$D$是不含美元, 如果$D不包含美元作为导出子子( di) 绘图。 Gy\ arf\ as- Sumner 的推测是简单图形上一个开阔的猜测, 它指出, 对于任何森林 $F$, 都有一些功能, 例如, 每张无价的图形$G$, 以美元计每张无价的图形$G$。 ( 方向的) $G$是无色的。 Aboulker, Charbit, 和 Naserasrarsr [Gy\ arf\' as- Sumner 的扩展是对Dirmjecture of Digraphics; E- JC 20211 提议, 此图的比方形图的比值比值比值比值比值比值为 。 dichal $D$$, 的比值是用于显示美元 美元( $美元) 美元的纸面的最小的颜色数。 $Drimaxx 美元, 美元, 美元是每张的直的值, 美元, 美元, 美元是每张的硬的值, 美元。