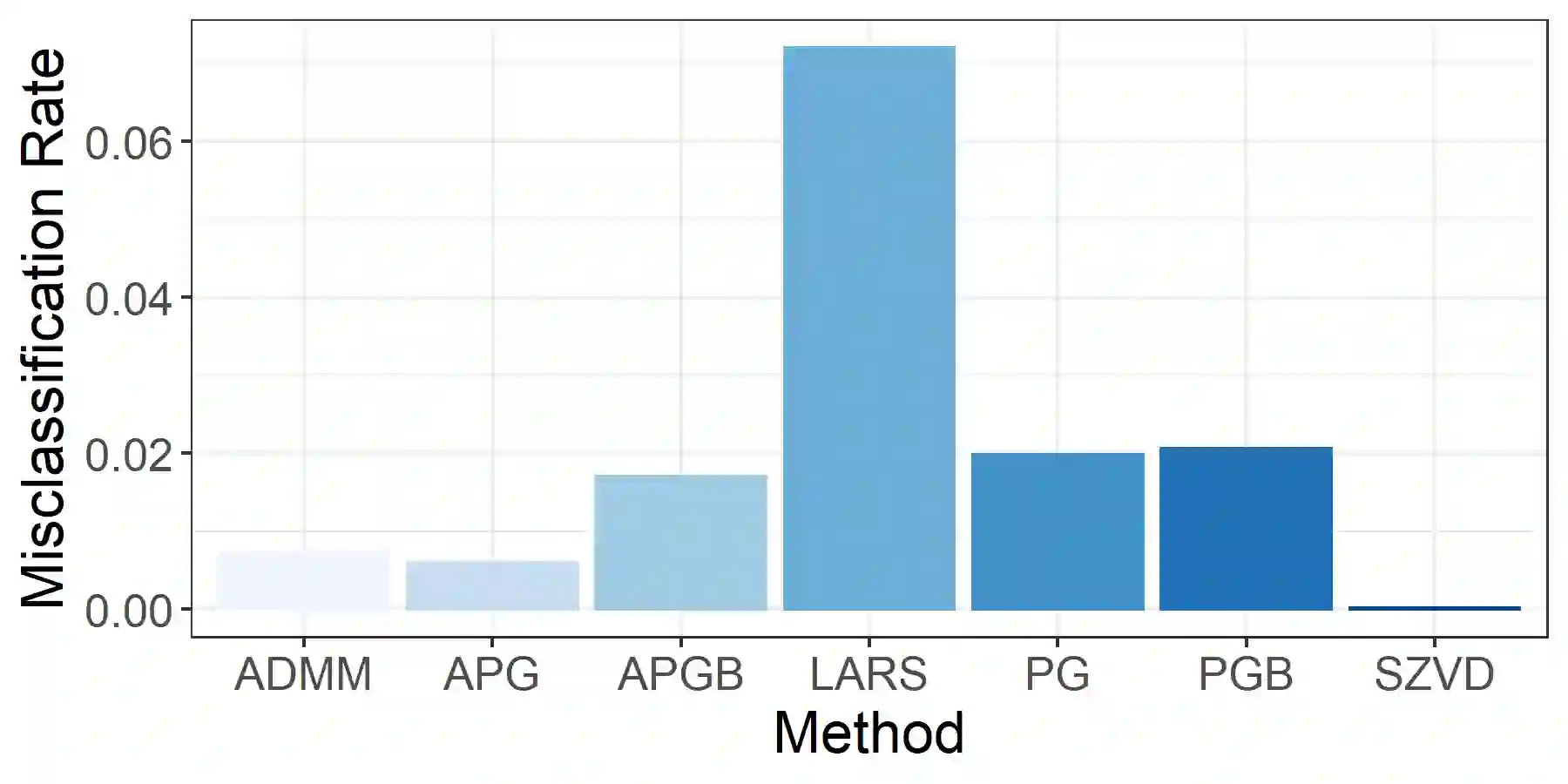
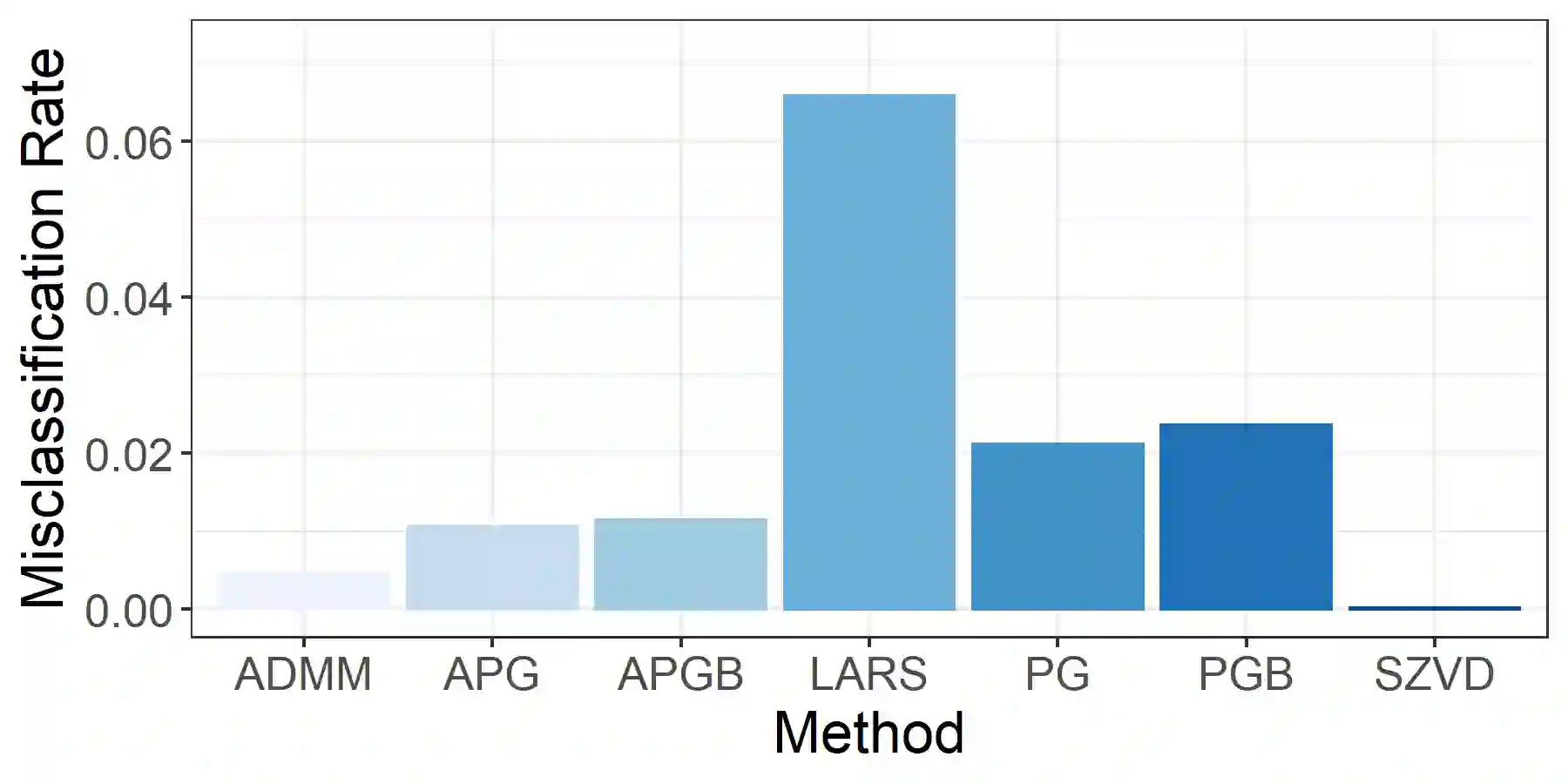
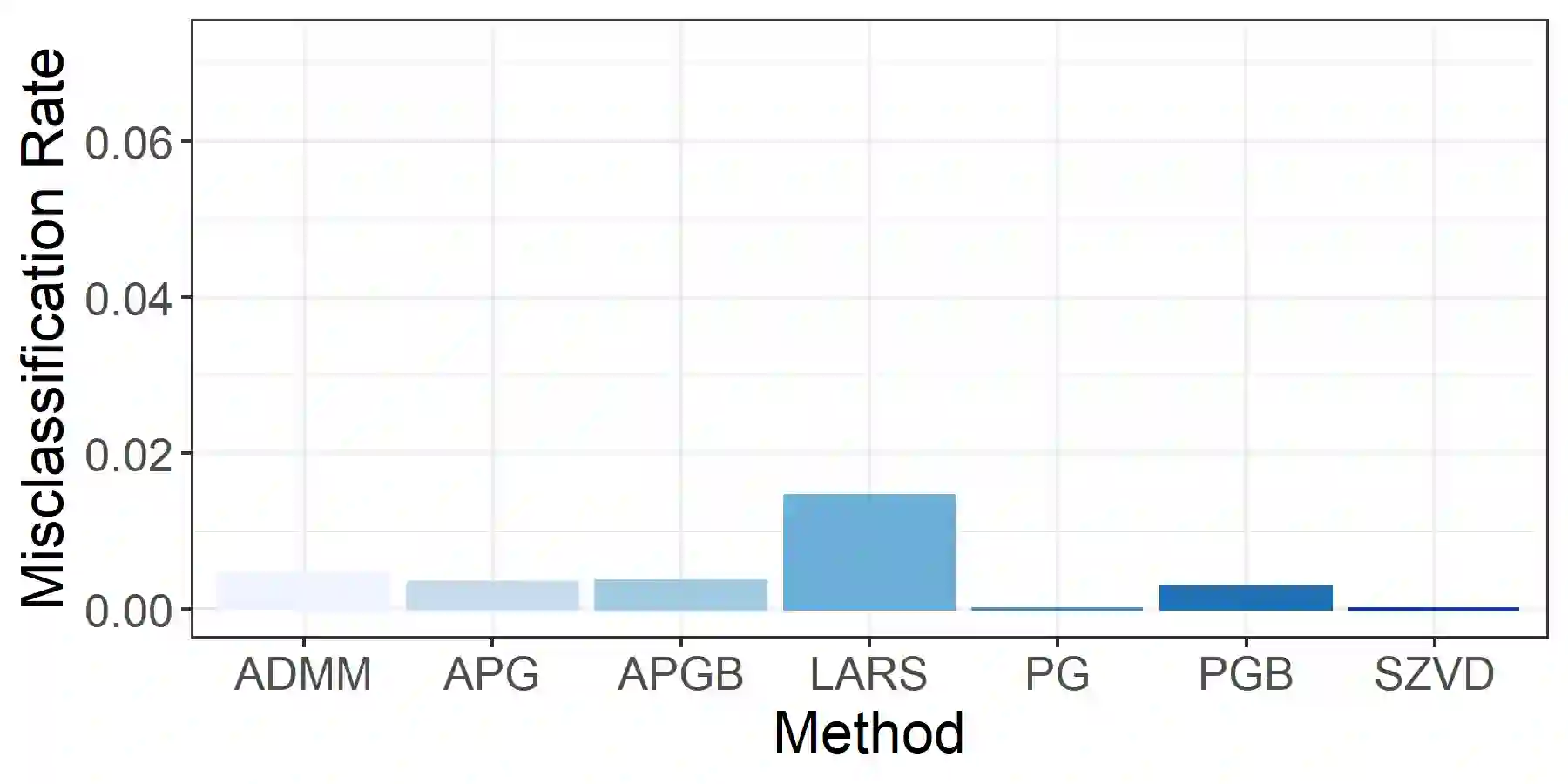
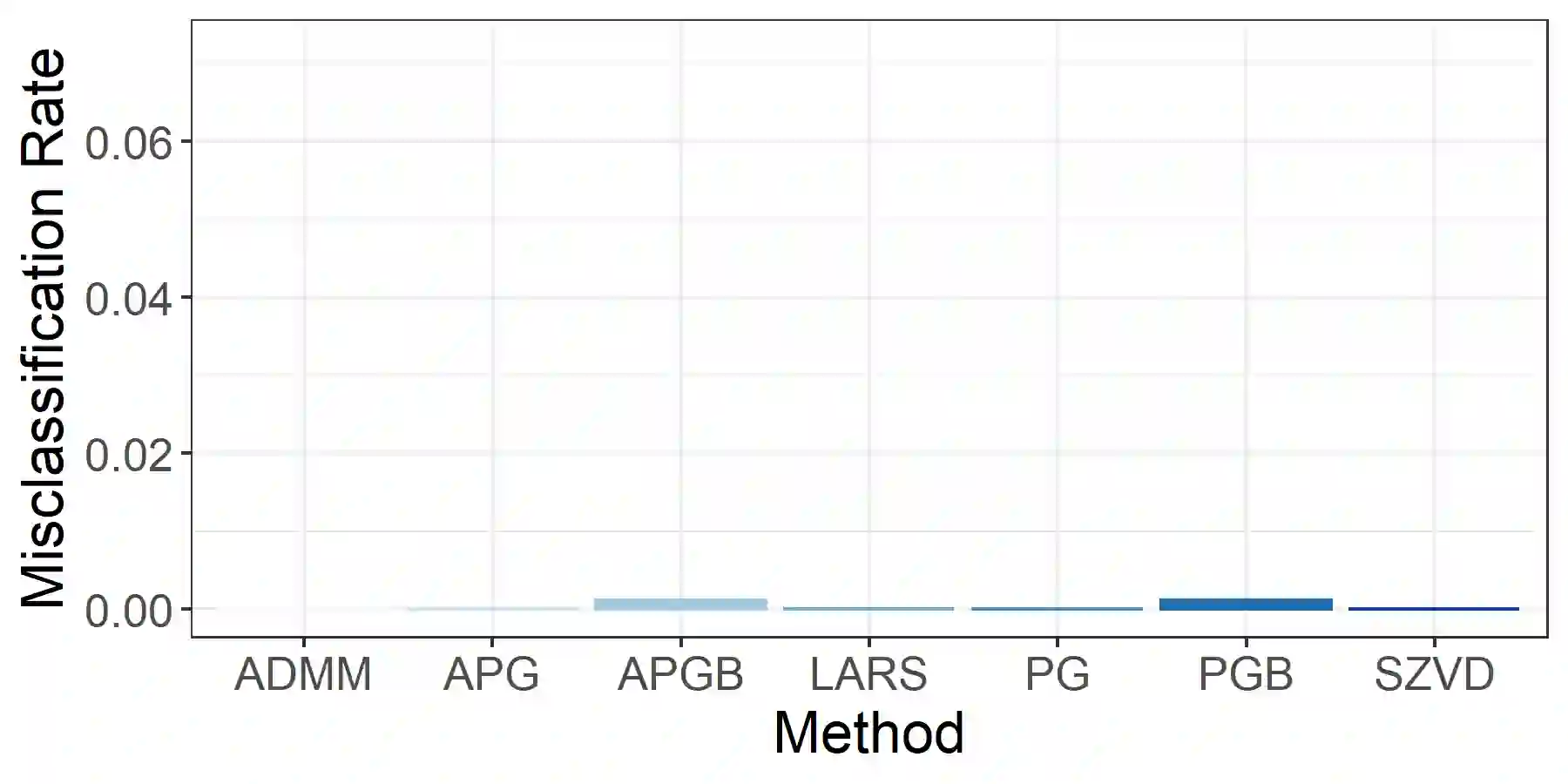
Linear discriminant analysis (LDA) is a classical method for dimensionality reduction, where discriminant vectors are sought to project data to a lower dimensional space for optimal separability of classes. Several recent papers have outlined strategies for exploiting sparsity for using LDA with high-dimensional data. However, many lack scalable methods for solution of the underlying optimization problems. We propose three new numerical optimization schemes for solving the sparse optimal scoring formulation of LDA based on block coordinate descent, the proximal gradient method, and the alternating direction method of multipliers. We show that the per-iteration cost of these methods scales linearly in the dimension of the data provided restricted regularization terms are employed, and cubically in the dimension of the data in the worst case. Furthermore, we establish that if our block coordinate descent framework generates convergent subsequences of iterates, then these subsequences converge to the stationary points of the sparse optimal scoring problem. We demonstrate the effectiveness of our new methods with empirical results for classification of Gaussian data and data sets drawn from benchmarking repositories, including time-series and multispectral X-ray data, and provide Matlab and R implementations of our optimization schemes.
翻译:线性线性线性分析(LDA)是一种典型的维度减少方法(LDA),它寻求相异矢量将数据投射到一个低维空间,以优化分类的分离性;最近一些论文概述了利用高维数据利用LDA的宽度利用高维数据的战略;然而,许多还缺乏可伸缩的方法来解决潜在的优化问题;我们提出了三种新的数字优化办法,以解决LDA基于块协调下降、准氧化梯度法和乘数交替方向法的稀疏最佳评分公式。我们表明,这些方法的渗透成本在所提供受限的标准化条件的数据的层面线性比例线性地计算,在最差的数据层面是线性计算。此外,我们确定,如果我们的区块协调下表框架产生相交汇的相交集的次序列,然后这些次序列会与稀薄的最佳评分问题的定点汇合。我们展示了我们新方法的有效性,通过经验得出了从基准储存库中提取的数据和数据集的分类结果,包括时间序列和多光谱谱系数据和数据。